 polydron その1
polydron その1

今、学部のゼミではグラフ理論関係のことを扱っているのですが、
いずれ多面体に関する内容へシフトしようと思っていまして、
大学の予算で ポリドロンという教具を大量に「大人買い」しました。
ポリドロンというのは、実際に手に取ってみると 見た目は いままでこのサイトで
紹介してきた
例の100円ショップで売っていた”3D geo shapesもどきと”と何ら変わりません。
ただ、材質が もうすこし かっちりした硬質のプラスチックになります。
#本物の”3D geo shapes”は 触ったことがないので分かりません。。
このポリドロンと 「あそびをせんとや」で紹介されている3D geo shapesは
どういう関係にあるのでしょ?出元は同じなんでしょうかね。
さて、先週の金曜日に大学に届きまして、この週末は自宅に持って帰り
いろいろ検討してみました。
最初につくったのは、立方体と正8面体の相貫体。

というのも 今回購入したセットには正多角形以外にも、
いくつかの三角形がはいっているのです。
基本となる正多角形のユニットの1辺の長さを1としたときに、3辺の長さが
(1、1、√2)の直角二等辺三角形、
(1、√2、√2)の二等辺三角形、
(√2、√2、√2)の大きめの正三角形、
がいくつか入っています。
さて、この後何を作ろうかなぁと考えていたら、家内が「ちょっといじっていい?」と
何やら作り始めました。彼女が作っていたのは小菱形立方8面体でしたが、
何やら色にこだわりたいらしく、困っています。このセットはどのパーツも
4色しかないので、4色できれいな配色を考えている様子。
しばらくして、彼女の完成品をみると なかなかの配色でした。

小菱形立方8面体の12個の「斜めの面」は 菱形12面体の12個の面と対応しますが、
ようするに彼女の配色は菱形12面体の面を4色で塗り分ける配色です。
それを図示すると、下図のようになります。

菱形12面体の頂点には次数4(辺が4本集まる)の頂点が6つと
次数3の頂点が8つありますが、上の配色では次数4の頂点の回りには
かならず4色が集まっています。
また、4つの色の巡回置換は4!/4で 6通りありますが、
この菱形12面体の6つの「次数4の頂点」のまわりに
その6通りの巡回置換がすべて現れています。
菱形12面体の面というのは、立方体の辺と1対1に対応します。
つまり 菱形12面体の面の塗り分けは 立方体の辺の塗り分けに
対応するわけですが、そのように図示したほうが分かりやすいかも
しれません。
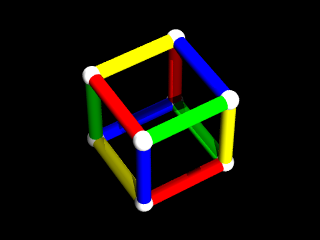
立方体の面の周りの辺の配色は 6通りの「4色の巡回置換」になっています。
さて、今回のポリドロンにも、さすがに菱形のパーツは含まれていない
のですが、家内の作った 小菱形立方8面体を見ているうちに
なんとか菱形12面体らしい形をつくりたくなりました。
いろいろ考えるうちに、正方形のまわりに正三角形をつけた形を
「菱形」と見立てれば、先端のとがった菱形12面体のような感じに
ならないかな?とおもい、作ってみたのが今回の形です。
配色は 先の菱形12面体の配色と本質的に同じです。
次数4の頂点の回りで、4色の出会い方は ひとつとして同じものがありません。

 もどる。
もどる。





