 紙の結び目2
紙の結び目2

hhase氏の
あそびをせんとや
の
3月18日のひとこと
にかいてあった次の結び目をみて、
是非ともこれをひと繋がりの紙で作ってみたい衝動に駆られました。
というのも、これは一見本当にほどけなさそうで、紙にかいて調べてみないと
なかなか頭の中でほどけるところを想像するのは困難なのですが、
なんとほどける結び目なのです。

さて、始めはあまり難しく考えずに、設計を考えました。
最初に考えたのはつぎのような用紙です。

|
| 図1 |
これを次のように折ると 交わりでの上下はともかく、
射影図としては 目的の結び目と同じになります。

あとは何とかうまいことやれば、目的の結び目になるだろう、、と
紙をこちゃこちゃ動かすのですが、一向にうまくいかない。
むむぅ。。
はて、何かおかしいぞ。これは、、、と考え直すことにしました。
結果論から申しますと、この最初の設計では目的の結び目は得られないのです。
結び目理論では、大まかに言って、上記のような
3次元空間内の自己交差しない閉曲線のことを
「結び目」といいます。
また、いくつかの結び目が互いに交わらないとき、これを「絡み目」といいます。
いま2つの結び目からなる絡み目を考えましょう。このような絡み目を
2成分絡み目といいます。2成分絡み目を成すそれぞれの結び目に向きを
定めます。向きとは それぞれの結び目をたどる方向のことです。
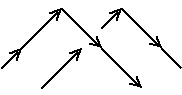
以下に 向きのついた2成分絡み目の例を載せます。
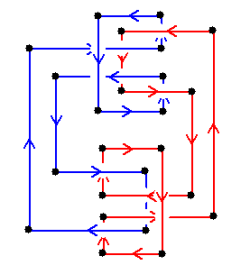
さて、向きのある2成分絡み目の図において、異なる成分の交点(上図でいうと
赤と青の線の交点)につぎのように符号を定めます。
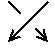 |
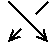 |
| +1 |
ー1 |
この符号の和は必ず偶数になることが分かっていまして、
その合計の半分の値をこの絡み目の「絡み数」と呼びます。
実は不思議なことに「絡み数」は 同じ絡み目であれば、
絡み目の図によらず一定なのです。
このことを使うとこの最初の設計がなぜ失敗だったのか分かります。
もし、この設計の用紙からつぎのように目的の結び目がつくれたとしましょう。

(切れ目を入れて無理やり作ってみました)
ここで、つぎのように紙の縁を2つの結び目と考えて、
2成分絡み目を考えてみます。

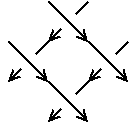
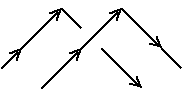
このとき、つぎの表のように紙が交差する部分では絡み数への寄与が向きによって+1かー1、
また紙が折れているところでは ±1/2となります。
#絡み数は 異なる成分の交点だけの符号和の半分であることに注意。
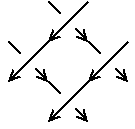 |
 |
| +1 |
ー1 |
 |
 |
| +1/2 |
ー1/2 |
さて、最初の図1をみてみると もともと紙の縁はまったく交差しないのでした。
ということは 出来上がった状態でも絡み数は0のはずです。
ところが、次の図のように
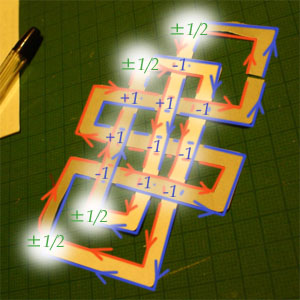
紙の帯の交差点での絡み数への寄与はー4。
一方、紙の折り目での絡み数への寄与は 最大でも+2なのです。
これでは うまくいきません。
つまり、ゴールの状態の「紙の縁からできる絡み目」で、
「紙の交差」部分だけで計算した絡み数がー4ですから、
トータルで絡み数0にするためには、紙の折り目がすくなくとも8ヶ所は
必要なのです。さらに、その8ヶ所がすべて符号が正となるように
折れなければいけません。
これに気付いて設計したのがつぎの用紙です。
 結び目の用紙:PDFファイル
結び目の用紙:PDFファイル
これは用紙のA、B、C、Dの場所で 2ヶ所ずつ好きな方向に折れるように
なっていますので、折り目での絡み数への寄与がー4から+4まで
変化させることができます。そういう次第で、トップの3種類の結び目、
(この3種は上部の2ヶ所の交点での上下だけが異る)がすべて折れるように
なっているというわけ。
興味のある向きは是非とも 実際に 印刷して3種類ともにチャレンジしてみてください。
知恵の輪に似たとても面白いパズルだと思います。
#本当はこれでは 目的の結び目を折れるための必用条件しか述べていませんが、
#目的の結び目が自明である限り ここで述べた条件を満たすように設計すれば
#かならずその結び目を紙でつくれることも 証明可能です。

 もどる。
もどる。














