過去の表紙119

立体魔方陣

まず、初めに断っておかないといけないのは、私は魔方陣に関しては全くの素人だということです。
当然、ここに書くようなことも古くから知られている事柄のはずですが、
文献にあたっていないので手頃な文献を知りません。

事の起こりは今年の春に卒業するＯ君の卒業発表でした。
Ｏ君は私のゼミの学生ではないのですが、彼の発表が魔方陣に関するもので、
彼が勉強した一様ステップ法という魔方陣の構成方法を紹介する内容でした。

魔方陣とは多くの方がご存じと思いますが、通常１からｎ²までの数を
ｎ×ｎの格子状に並べて、ｎ個の列及びｎ個の行の和が等しくなるようにしたものです。
定義によっては「対角線の和も等しくなるように」とする場合もあるようですが、
ここでは対角線は考えないことにします。

次は一様ステップ法で構成した魔方陣（ｎ＝３）の例です。
ただし、ここでは１からｎ²の数ではなくて、０からｎ²ー１の数を使っています。
（ちなみに、一様ステップ法ではうまくやれば、対角線の和も考慮することも可能です）

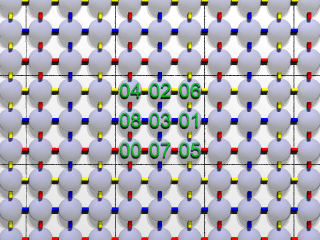
図１：一様ステップ法による魔方陣

各行、各列の和が１２になっているのが見て取れるでしょうか。

さて、これはどのようにして作られたのかを説明していきましょう。
まず、次のように０から８の数字が順に並んでいるところを考えます。

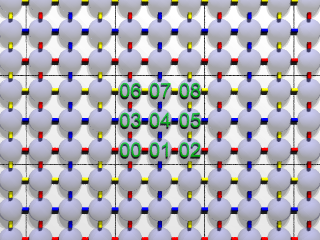
図２：初期配置

左から右へ、下から上へときれいに並んでいます。
もちろん、この状態では魔方陣になっていません。

次に上の状態から数の並びを「一次変換」するのです。
一次変換が何か、、、を言葉で説明するより見てもらった方が話が早いでしょう。

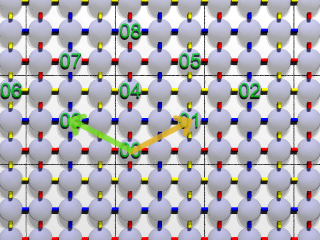
図３：一次変換

上の画像をみれば大体理屈は分かってもらえると思うのですが、
図２の初期配置では、００から０１へ移るときは右に一つずれていました。
図３では右に１つ移動する変わりにオレンジの矢印で示したベクトルだけ移動しています。
また、図２の初期配置では上に１つ移動する部分が、
図３では緑色のベクトルだけ移動しています。
右方向をｘ方向、上方向をｙ方向として座標を考えれば、

オレンジのベクトル＝（２、１）、緑色のベクトル＝（ー２、１）

となります。この２つのベクトルの選び方が重要なのですが、それは後述。

さて、図３では数字があちこちに散ってしまっていますから
もとの正方形のなかに収まるように戻します。そのとき、白い正方形のなかでの位置を変えずに
戻します。つまり図でいうと縦の赤いライン上にある数は、戻した先でも縦の赤いライン上に、
という風に戻します。

すると、図１の魔方陣が得られるのです。

さて、上でベクトルの選び方が大事だと言いましたが、正確にはオレンジのベクトル＝（ａ、ｂ）、緑色のベクトル＝（ｃ、ｄ）としたときに、
ａｄ－ｂｃ，ａ，ｂ，ｃ，ｄの５つの数字がすべて、ｎと互いに素（今の場合ｎ＝３）
でないとダメです。

なぜ、この方法で魔方陣が得られるのでしょうか？
それを見るためには数をすべてｎ進数（今の場合は3進数）で書くと分かりやすくなります。

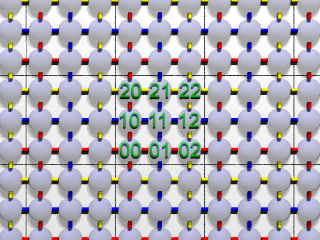
図４：初期配置（3進数）

上は初期配置の状態を 3進数で表したものです。
これを下のように 1次変換して、、、

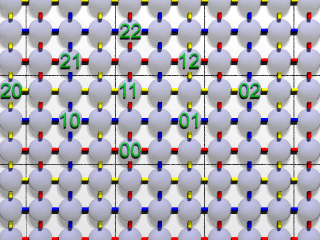
図５：

さらに、元の正方形のなかに収まるように戻すのでしたね。
この戻す作業をするときに、２つ以上の数が同じ位置に来ないようにするためには、
ａｄ－ｂｃがｎと互いに素であることが必要なのです。

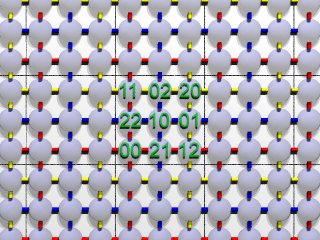
図６：一様ステップ法による魔方陣（3進数）

さて、列や行に並ぶ数をみてください。
どの列や行を見ても、１０の位、１の位に０、１、２が１つずつ現れています。
とすれば、列や行の和が等しくなるのもうなずけます。
このように、ｎ進数で表した際、
各行、各列の数の「１０の位」、「１の位に」、０からｎ－１が１つずつ現れる
ようにするために、ａ，ｂ，ｃ，ｄがｎと互いに素であることが必要なのです。

ここまでが、Ｏ君の発表内容でした。(ただし、説明方法は大幅に変えています。) なかなか面白い内容でした。
そして、発表を聞いてる最中から、これはこのまま３次元に拡張できそうだぞ、
という考えが湧いてきて、ムズムズしていました。理論的な検証への欲求よりも、
うまくいきそうだという直感とそれを形にしてみたいという欲求につき動かされて
その夜 povrayで画像を作れるように povファイルを書きました。

基本的にはやっていることは 2次元のときと何も変わりません。
０からｎ²ー１までの数字をきれいに並べて、適当な１次変換をしてから、
もとの立方体へ戻すだけです。
ただ、1次変換の選び方が難しい。はじめはよく分かっていなくて、
各面、、というか、正方形状の断面の部分の和が等しいというものになってしまいました。

下の図７では、

一番上の段の和：１０＋０７＋２２＋１５＋０３＋１８＋１４＋０２＋２６
真ん中の段の和：２０＋１７＋０５＋２５＋１３＋０１＋２１＋０９＋０６
一番下の段の和：００＋２４＋１２＋０８＋２３＋１１＋０４＋１９＋１６

が等しくなっています。同様に手前の面や右の面も同じ和です。
でも、列の和は等しくなっていません。

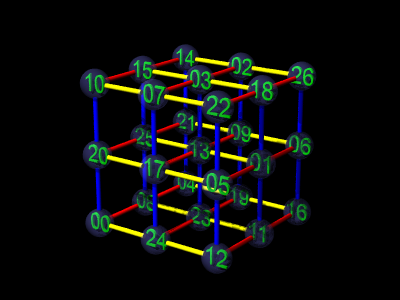
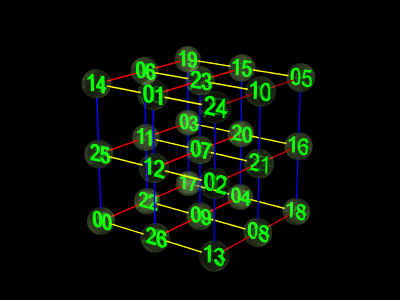
図７：立体魔方陣？

図７では 1次変換を示すベクトル（ｘ，ｙ，ｚ座標にそった基本ベクトルの移る先）として、

（２、１、１）、（１、１、２）、（１、２、１）

を使っています。
（図で００から２４へ進む方向、０８へ進む方向、２０へ進む方向をそれぞれｘ軸、ｙ軸、ｚ軸の方向として説明しています）

これだと、たとえば手前の一番下の部分に００、１２、２４が並んでいますが、
この３つの数はすべて３で割りきれる（3進数で表すと１の位が全部０）ことになってしまいますので、
すべての列の和が等しくはなりません。
（ややこしくなるので詳しくは述べませんが、これは上記の３つのベクトルのうちの、
2番目と3番目のベクトルを足すと（２、３、３）となり３を法とする合同式で考えると（２、０、０）、
つまり、座標軸に沿ったベクトルになってしまったことに起因します）

それに気付いて、改良したものが次の立体魔方陣です。

図８：立体魔方陣（サイズ３）

図８では 1次変換を示すベクトルとして、

（１、０、２）、（０、２、１）、（１、１、０）

を使っています。

原理に気付けば、一般化することは簡単でした。
次の画像はサイズｎ＝５の立体魔方陣です。

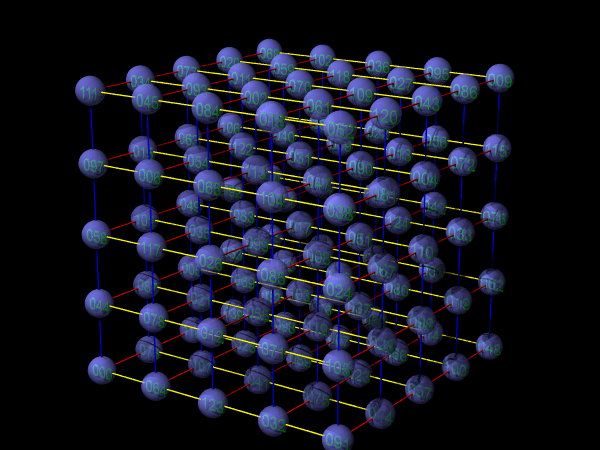
図９：立体魔方陣（サイズ５）

もどる。