 リングの蟻継パズル
リングの蟻継パズル

上の画像のトーラス(=ドーナツ上の形)は5つのパーツが蟻継ぎによって 繋がって出来ています。
蟻継ぎとは ジグソーパズルのピースとピースを繋ぐときのような形で、
木材と木材を繋ぐ方法のことです。(種々の方法があるようですが、今回のは一番簡単な継ぎ方)
蟻継ぎの方向は 5つの繋ぎ目で全て異なるようになっています。具体的にいうと
リングをたどっていくと、繋ぎの方向が少しずつずれていって、一周したときに
ちょうど180度回転して 元に戻るようになっています。
繋ぎ目の方向が全て異なるので、ぱっと見ると 外すことが出来なさそうな気がします。
さてさて、この物体、うまく5つのパーツに分解することが出来るのでしょうか?
きちんと数学的に考えてみましょう。次の図のように5つのパーツに名前をつけます。
実はPとQは動かないままで この物体をパーツに分解することが可能なのです。
まず、Aについて考えてみますと、Pは動かないので、Aは蟻継ぎの部分に沿った動き
つまり、次の図の黄色い矢印xに沿った動きしかできません。
次にパーツBについて考えてみますと、BとAはやはり蟻継ぎによって繋がっていますから、
Aに対するBの相対的な移動方向は やはり図に書き込まれた黄色い矢印yの方向になります。
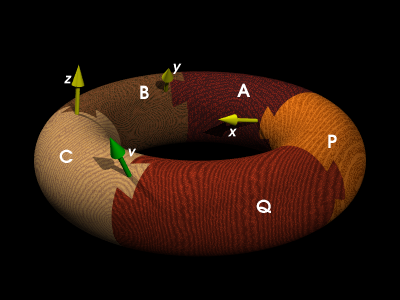
同様に パーツCの パーツBに対する相対的な移動方向も図に書き込まれた黄色い矢印zの方向になります。
ここで、
パーツAがベクトルxのs倍で動き、パーツBがパーツAに対してベクトルyのt倍で動き、
パーツCがパーツBに対してベクトルzのu倍で動くとすると、
パーツCの動きは これらの合成つまり sx+ty+uzで動くことになります。
さて、パーツQも動かないと言いましたから、QとCの繋ぎ目部分について考えれば
パーツCの動きは緑色のベクトルvに沿った動きでなければ行けません。
結局問題は次のようになります。ベクトルx,y,zをスカラー倍して足し合わせたものが
ベクトルvに等しくなるように出来るか? 線形代数の用語を使えば、
vをx,y,zの一次結合で表すことができるか?ということです。
実は このときx,y,zは一次独立なので、いかなる3次元ベクトルでも
x,y,zの1次結合として表すことができます。
つまり、3つの黄色いベクトルに沿った動きの大きさを上手く調節すれば
同時にパーツA,B,Cを動かして 外すことが出来るというわけです。
下の画像にマウスで 触れると 実際に外すところをみることができます。
(ちょっと重たいかもしれませんが。。)

 もどる。
もどる。


