 曲がったタイリング
曲がったタイリング

今回の画像は2つの異なった方法で解説することにします。
まず、タイリングを使った説明から:
つぎのような特殊な方法で三角形のタイルを平面に敷き詰めることを考えます。
まず、三角形を1つ描いて(図の黄色の三角形)、その三角形を
辺を対称軸としてパタンと鏡映すると3つの裏返しの三角形ができます。(3つの青い三角形)
それらの三角形をさらに辺でパタンと裏返すと今度はおもての三角形が増えます。(オレンジ色の三角形)
さらに それらの三角形を、、、と繰り返すのです。
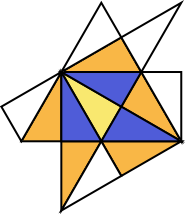
このようなタイリングを鏡映タイリングと呼ぶことにしましょう。(正式名は知らない)
ただし、ここでは裏の三角形と表の三角形が常に隣り合わせになるという条件をつけます。
だから頂点の回りに奇数個の三角形が集まるのはダメです。
当然、いつでもそのような方法で、きれいにタイリングが出来るわけではなくて、
いまの場合でいうと三角形の3つの角が180度を自然数で割った角度でないとだめです。
そうしないとうまくいかずにタイルとタイルが重なってしまったりするのです。
三角形の内角の和が180度なので、ちょっと計算すると、
このようなタイリングが出来る三角形は正三角形、直角2等辺三角形、と、
3つの角が30度60度90度の三角定規の三角形だけだということがすぐ分かります。
でも これだけでは 面白くない。
そこで、次のような曲がった三角形を考えます。つまり、3つの辺が
線分ではなくて弧で出来ている『三角形』を考えるのです。
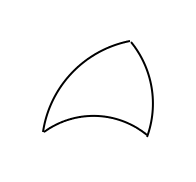
今回は辺が曲がっているので「辺を対称軸として、鏡映する」が使えませんから、
その代わりとなる何か代替物が必要です。そこで円に関して鏡映するという概念を使います。
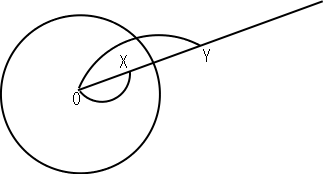
次の図のように円Oの中心から伸びる半直線上の点X,Yが
|OX|×|OY|=(円の半径)2
を満たしているとき XとYはこの円に関して対称といいます。
これを使って点を円に関して対称な位置に写す写像を円に関する鏡映とするのです。
円に関する鏡映がどんな動きをするかを示す簡単なアプレットをシンデレラで
ここに作っておいたのでお試しあれ。
ところで、この円に関する鏡映は 「弧を鏡映するとまた弧になる」という性質を持っています。
ですから、「曲がった三角形」をその辺(弧)に関して鏡映すると、また「曲がった三角形」になります。
ということは、円に関する鏡映を使うと、上記のような曲がった三角形を出発点として
次々に辺(弧)に関して鏡映することで、やはり鏡映タイリングをつくることができます。
もちろん、どんな「曲がった三角形」でも うまくタイリングが
できるわけではないのですが、実は 曲がった三角形の3つの内角がすべて
180度を自然数で割った角度になっていれば、うまいこと鏡映タイリングができることがわかっています。
さて、では 曲がった三角形から鏡映タイリングを作ると一体どうなるでしょう?
今回の画像はそのような曲がった三角形からできる鏡映タイリングの1つなのです。
トップの画像に現れる「曲がった三角形」は 内角がすべて36度、60度、90度になっています。
次に球面上のタイリングの話:
一方で 今回のトップ画像は次のようにしても得ることができます。
#っていうか 以下の方法で計算して作っています。
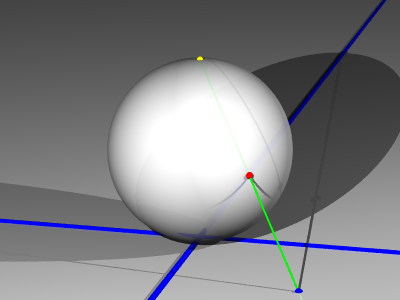
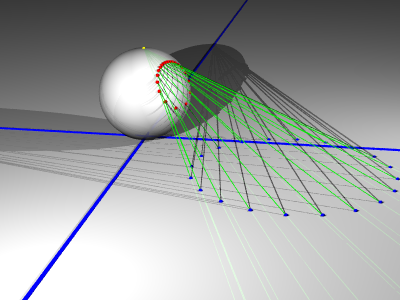
まず、立体射影について説明しましょう。つぎの図のように 平面と、
この平面に接する球面を考えます。平面と球面の接点を南極と呼ぶことにして、
球面上の南極と反対側の点を北極(図の黄色い点)と呼ぶことにしましょう。
球面上の北極以外の点X(図の赤い点)に対して、北極とXを結んだ直線が平面と交わる点を
f(x)(図の青い点)とすると、fは(北極を除く)球面から平面への写像になります。
この写像を立体射影と言います。
この立体射影は色々と面白い性質があります。例えば、球面の上の円を立体射影すると、
どうなるでしょう?ちょっと頭の中で想像すると、卵型のような形になりそうなものですが、
次の図のように立体射影は 球面上の円を平面状の円(もしくは直線)に移します。
さて、次の図をみてください。手鞠模様のように球面上に三角形が並んでいますが
この模様は15個の大円(球面の中心を通る平面で球面を切った時に出来る断面)で出来ています。

それら15個の大円を上に述べた立体射影で 平面に写すとどうなるでしょうか?
それが今回のトップ画像 ということも出来るのです。
何故、曲がった三角形のタイリングが球面上のタイリングになってしまったのでしょうか?
実は いつでもそうというわけではありません。
そこには 非ユークリッド幾何学の面白い仕掛けが潜んでいるのです。
 もどる。
もどる。






