 Hopfファイバー束
Hopfファイバー束
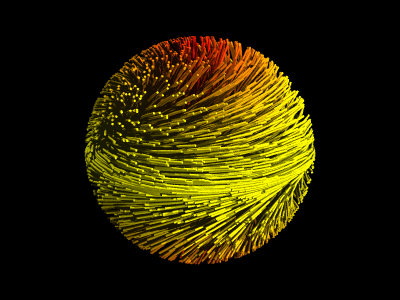
はてさて、今回はHopf写像の図なので、Hopf写像の解説を
書かないといけないのですが、どこから どうやって説明しようか。
なるべく難しいことを言わずに書いてみようと思います。
まず 円周を考えましょう。円周のことを「1次元球面」と呼びます。
1次元球面(=円周)は 次のように 2つの半円を繋いだものと考えることができます。
さらに 柔らかい幾何学=トポロジーでは半円と線分は同じものです。
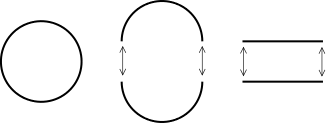
そう考えると 1次元球面とは 2つの線分を繋いだモノと考えることができます。
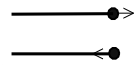
つまり線分が2つあって、片方の線分から外に出ようとすると
もう片方の線分に入ってくる。そういう世界が 1次元球面なのだ、
と考えることができますね。
つぎに いわゆる 一般に呼ばれるところの普通の球面を考えましょう。
この「球面」のことを 私たちトポロジストは 「2次元球面」と呼びます。
2次元球面は 次のように2つの半球を繋いだものと考えることができます。
上記と同様、トポロジー的には 半球と円盤は同じものです。

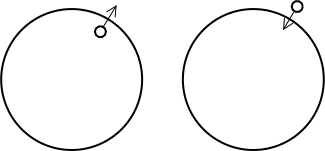
そう考えれば、1次元の時と同様、2つの円盤を繋いだものが2次元球面と言えましょう。
すなわち、下のように 2つの円盤があって、片方の円盤から外に出ようとすると、
もう一方の円盤の丁度同じ場所に入ってしまう。そういう世界が2次元球面なのです。
さて、ようやく「3次元球面」を考えます。
ところが、「3次元球面」というのは 絵が描けないのです。
そこで、上に書いた手法で 「3次元球面」を捉えることにしましょう。
つまり、3次元球面とは
2つの球体があって、片方の球体から出ようとすると もう一方の球体の
丁度対応する場所に入ってしまう、そういう空間なのです。


「3次元球面」について 分かってもらった上で、最初の画像に戻ります。
最初の画像を「3次元球面の半分」と思ってください。
つまり もう一方の片割れと対にして考えます。
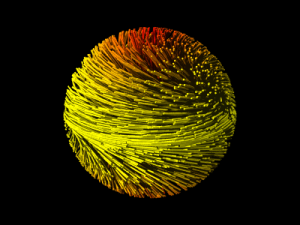
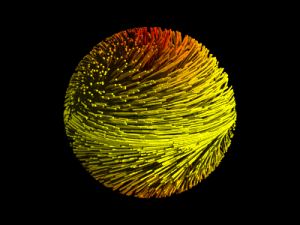
すると たくさんの曲線は 「一方の半分」から出て、
そのまま「もう一方の半分」に繋がるようになっています。
そうして、「もう一方の半分」に入った曲線は しばらく進むと また 外に出て、
「もとの半分」に入ったところで 最初の曲線に繋がっています。
つまり これらの「たわし のような図(笑)」は 3次元球面上の たくさんの
閉曲線を表しています。
これらの閉曲線の群れをすべて考えると、
3次元球面上のどの点に対しても、その点を通るただ1つの閉曲線があるのです。
これらの閉曲線群は 次のように構成されています。

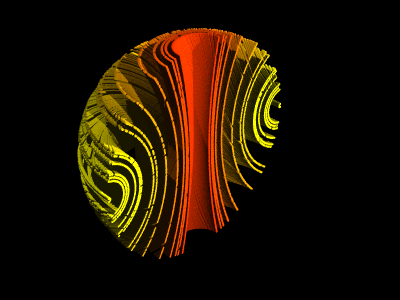
上図の様に まず球体を「筒」の集まりと考えます。(右が断面図)
赤い部分は 縦長の筒、黄色い部分は赤道を周回する筒を半分に削ぎ切りしたように
なっています。
これらの筒は 「もう片方の半分」と繋がることで トーラス(ドーナツの表面)に
なります。ただ2つだけ例外があって、
・球体の南極と北極を繋ぐ軸は線分なので、「もう片方の半分」と繋がって円周に、
・球体の赤道は円周で、「もう片方の半分」の円周と重なって円周に、
なります。最後に トーラスの表面を
「トーラス上を螺旋状にめぐる(1回転する間に一周する)斜めの閉曲線」の群れで
覆い尽くせば 出来上がり。
これが有名な(?笑)Hopf ファイバー束ってやつです。
これ以上は 説明が難しいので、結果だけになりますが、
各閉曲線を1点につぶすように「射影」しますと、2次元球面が得られるのです。
この3次元球面から2次元球面への『射影』がHopf写像で、
Hopf写像においては、1点の逆像はつねに1次元球面になります。
 もどる。
もどる。










