過去の表紙99

多面体のグラフの球面上コイングラフ表現

忙しくてなかなか解説ページが書けませんでしたが、
今日は仕事をする気になれない一日でしたので、(って、休日ですけどね)
思い切って説明用の画像をいくつかつくりました。

過去の表紙92で一般化したpropellor 作用素を施した多面体のCGを載せましたが、
何が大変って canonicalization が大変なのでした。canonicalizationとは
与えられた多面体をもっとも「自然な形」に変形することです。
具体的には
１）面はすべて平らで、
２）辺はすべて単位球面に接し、
３）頂点の重心は原点に一致する。
というものでした。単位球面に外接、内接ではなく、
「すべての辺が単位球面に接する」という２番の条件が面白いです。
実際に canonicalizeしたp-立方体と「単位球面」を描いてみますと、
つぎのようになります。

ところで、一つの頂点に着目するとある点から単位球面へ接線を引いたとき、
接点までの距離は常に一定です。

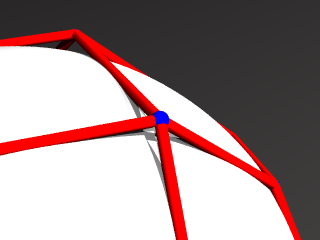
ということは、各頂点を中心として、「その点から単位球面へ引いた接線の接点までの距離」を
半径とする球面を描くと、辺で繋がった２つの頂点に対応する２つの球面は必ず接するようになります。

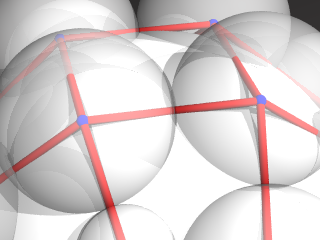
かくして、canonicalizeした多面体に対応して、
各頂点を中心にもつ球の一群で、「多面体の辺がつなぐ２つの頂点を中心とする２つ球面が必ず接する」
という性質をもつものをとることができます。

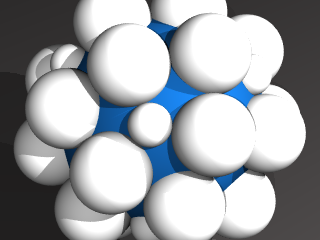
これらの球体群を単位球面で切り取れば最初の画像になるというわけ。

「頂点の集まり」と「頂点同士を繋ぐ辺の集まり」の成す組み合わせ構造のことをグラフといいます。
グラフの各頂点に対応して、円をひとつずつ描き、
「頂点が辺で繋がっている」⇔「対応する円が接する」
となるようにできるとき、それらの円の集まりをグラフのコイングラフ表現といいます。
今回の図は canonicalizeされた多面体は自然に
多面体のグラフの「球面上のコイングラフ表現」を与えるということを表しています。

さて、他の多面体についても同様の構成を行った画像を載せます。
各円の中心にもとの多面体の頂点があると思うと、元の多面体が見えてきます。

これは P_2+3i-正12面体の球面上コイングラフ。

これは propellor-正12面体の球面上コイングラフ。

これは propellor-正20面体の球面上コイングラフ。

もどる。