generalized p-operator : P(2+3i)









過去の表紙76, 77にて 立方体を斜めに編むということと、
G.W.Hart氏の述べる propellor-作用素 との関係を書きました。

また、過去の表紙78にて propellor作用素はもっと一般化できることを
説明しました。そこでは ガウスの整数環（を単元群で割ったもの）の元に
対応して、一般propellor作用素が定義できるということを述べたのでした。

しかし その作用素で出来る多面体のCGを描くことは ちょっと大変だったので
過去の表紙78では 一般 p-作用素で出来る多面体に対応するグラフを
正１２面体上に描くに留まりました。

いつか ちゃんとCGを描いてみたいな、と思っておりまして、
このところ その作業のためのプログラミングをしていたんですけども、
まぁ プログラミングは本業ではないんで、ずいぶん時間がかかってしまいました。

次の図は 「P(4+6i)正8面体」ですが、


左の図のように 一般P作用素は元の多面体の上の格子模様から定義されます。
ですが これでは 「面」が平らではありません。
右は単に頂点が球面上にくるように「膨らませた」ものですが、
もちろんこれでも 「面」が平らではありません。

このあと、面が平らになるように”canonicalization”してやる必要があるのです。

ある凸多面体Ｋに対して（もっと一般に３連結な平面グラフＫに対して）
そのcanonicalizationＬとは （Ｌは凸多面体）

０）Ｌの「面」は当然平面上にあって、
１）Ｌは辺や面の接続具合いがＫと全く同一で、
２）Ｌの辺はすべて単位球面に接し、
３）Ｌの頂点の位置ベクトルの平均が原点（頂点集合の重心が原点）

となるものです。そのようなＬがＫに対して（合同を除いて）ただ１つあることが
知られています。 （凸多面体の数学；G.M.ツィーグラー シュプリンガーフェアラーク東京）


canonicalizationするには

V）ラベル付された各頂点の座標
E）各辺がどのラベルの２つの頂点を結ぶか、
F）各面の回りを正の向きに一周するときの頂点のラベルの巡回列

の情報を求める必要があります。
とくにF）がめんどくさい。。

上の「P(4+6i)正8面体」の図は プログラムを作る途中経過の図ですが、
赤くなっている面がすでにF）の情報を求めた部分でした。

格子模様は過去の表紙78で述べたように 三角形上の格子を貼り合わせて作るので、
三角形と三角形を繋ぐ辺の部分が 一番やっかいなのです。でも どうにかこうにか
プログラムが完成して 公開に至りました。 たとえば 上のP(4+6i)正8面体を canonicalizeすると次のようになります。



辺に妙なゆがみや緊張がなくなり、自然な形になっています。美しい！


とにかく パラメータを変えればいくらでも 多面体のCGが出てくるわけですが、
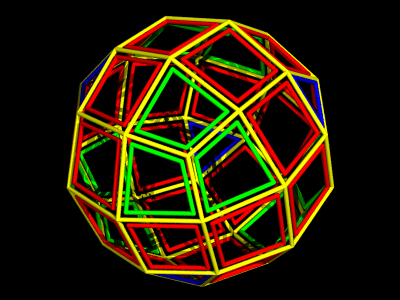
今回はP(2+3i)作用素を
使ったものにしましょう。
(2+3i)はガウス整数環の素元なので 他の単純な作用素の積では
書けないと思います。

以下の図では 元の多面体の頂点の回りの面が黄色に、
元の面の中心付近の面が緑になっています。


P(2+3i)正４面体
P(2+3i)正６面体 P(2+3i)正８面体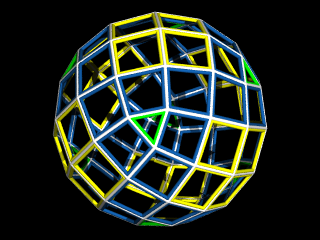
P(2+3i)正12面体 P(2+3i)正20面体
上図を見ると P(2+3i)は 双対を取ることと可換なのかな、と気付きます。
もどる。