過去の表紙78

generalized p-operator

帯で編むという事から離れて、前回立方体に対して考えたことを
一般の多面体に対して行うことを考えてみます。
その中で、G.W.Hart氏のp-作用素の一般化を考えたいのです。
とりあえず帯のことは忘れて、単なる格子として次の模様を考えます。

まず正方形の辺を５等分して対辺の等分点と３つずつずらして、
正方形上に格子模様を考えます。
この模様を正方形上の３＋５ｉの格子模様と呼びましょう。
（例によって－１やｉを複素数に掛けても格子模様は変化しません。）

この正方形の真ん中の点と辺の両端でできる三角形の部分を考えます。
これを三角形上の３＋５ｉの格子模様といいましょう。
直角２等辺三角形でないときは適当に１次変換することで
どんな三角形に対してもこの格子模様を考えることができます。
（頂角を指定する必要がありますけども）

最後に凸多角形に対して、その内部の点と頂点を結んで
三角形に分割し、それぞれの三角形ごとに上記の格子模様を
適当な向き（頂角が中心にあつまるように）で描くと、
凸多角形にも格子模様ができます。これを
凸多角形上の３＋５ｉの格子模様と呼びましょう。

正方形の3+5iの格子

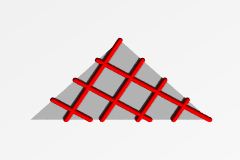三角形の3+5iの格子

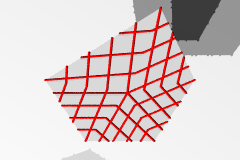多角形の3+5iの格子

つぎに正方形の辺を５等分する等分点を辺の長さの５等分のさらに半分だけ
ずらして対辺の等分点と３つずつずらして結ぶ格子模様を
正方形上の３＋５ｉの双対格子模様と呼びましょう。

この場合も４分の１の直角２等辺三角形に模様を制限したものを
三角形上の双対格子模様とします。

凸多角形にたいしても上記と同様に三角形に分割してから
それぞれの三角形に上記の三角形上の双対格子模様を描いたものを
凸多角形の双対格子模様とします。

3+5iの双対格子

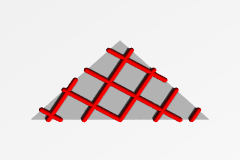三角形の3+5iの双対格子

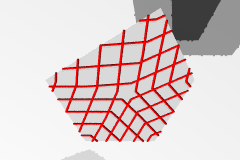多角形の3+5iの双対格子

もちろん３＋５ｉ以外の複素整数に対しても同様に格子模様を定義するわけです。
以下にｉ，２＋３ｉ，１＋７ｉの格子模様を載せます。

	0+i	2+3i	1+7i
正方形上の格子
正方形上の双対格子
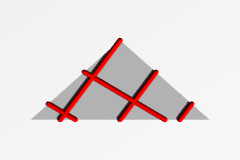
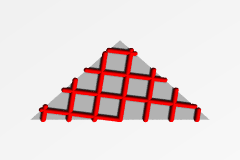
三角形上の格子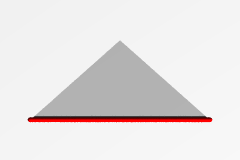
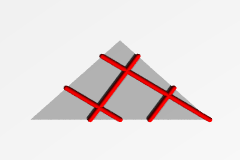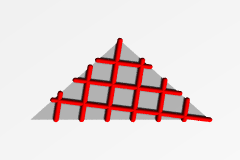三角形上の双対格子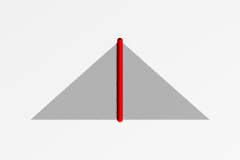
多角形上の格子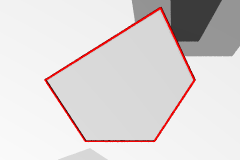
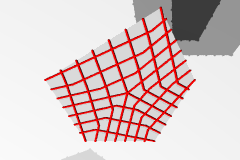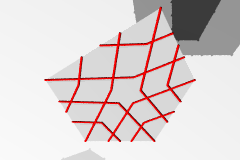
多角形上の双対格子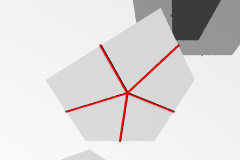

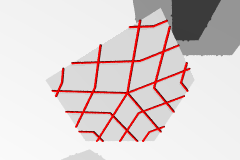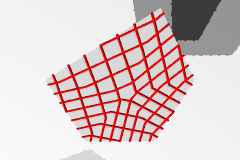さて、一般の（各面が凸多角形の）多面体と複素整数ａ＋ｂｉに対して、
上記の方法で各面に格子模様を描くと多面体上に格子模様ができます。
この格子模様の線が3本以上あつまるところを頂点として、
頂点と頂点を結ぶ格子の折れ線を辺とすると、これは１つの球面グラフでは
ないか、と。しかも３連結なので、凸多面体グラフになると思うのです。

つまりこの模様は１つの凸多面体の面のつながり具合いを表しています。

そこで与えられた多面体Ｘと実部虚部が整数の複素数ａ＋ｂｉに対して、
上の操作でできる格子模様が表す（組み合わせ）多面体をＰ_ａ＋ｂｉＸ、
上の操作の双対格子模様が表す（組み合わせ）多面体をＰ^*_ａ＋ｂｉＸ、
と書くことにしましょう。

現在の予想として、次が成り立つんじゃないかな、と思っています。

α、βは実部虚部が整数の複素数、Ｘは面が凸の多面体として、
Ｐ_αＰ_βＸ＝Ｐ_αβＸ
Ｐ^*_αＰ_βＸ＝Ｐ^*_αβＸ
Ｐ_１Ｘ＝Ｘ、Ｐ^*_１Ｘ＝ｄＸ
（ｄはdual,つまり双対をとることを表す）
Ｐ_１＋ｉＸ＝ｊＸ、Ｐ^*_１Ｘ＝ａＸ
（ａはambo、つまり角を辺の中点まで切り落とすことを表す）
（ｊはjoin、つまり amboとdualの合成を表す）
Ｐ_１＋２ｉＸ＝ｐＸ、Ｐ_１－２ｉＸ＝ｐ'Ｘ
（ｐはpropellored、右ねじりのp-操作を表す）
（ｐ'はpropellored、左ねじりのp-操作を表す）

（Ｐ_αＰ^*_βＸやＰ^*_αＰ^*_βＸについてはよく分かりません。）
以下に正１２面体に対して、上のＰ_ａ＋ｂｉ、Ｐ^*_ａ＋ｂｉを施した格子模様を載せます。

	Ｐ_ａ＋ｂｉ	Ｐ^*_ａ＋ｂｉ
a+bi=0+iのとき（a+bi=1のときと同じ）	P₁は何もしません。	P^*₁は双対になります。
a+bi=1+iのとき	P_1+iは joinです。この模様は菱形３０面体を表しています。	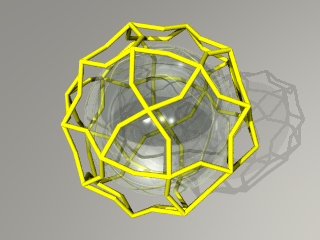P^*_1+iは amboです。この模様は１２面２０面体を表しています。
a+bi=0+2iのとき	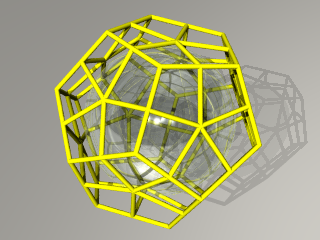この模様は凧型６０面体を表しています。	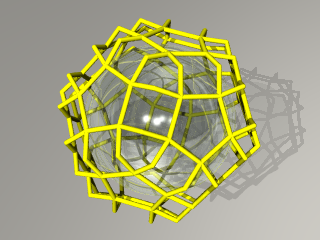この模様は小菱形12面20面体を表しています。
a+bi=-1+2iのとき	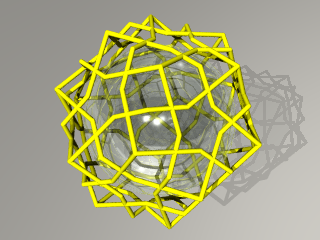p'-12面体を表しています。	p'-20面体を表しています。
a+bi=2+2iのとき	2+2i=2(1+i)=(1+i)2なので、菱形３０面体の各面を４分割したとも考えられるし、凧型６０面体のjoinとも考えられる。	P^_2+2i= P^_1+iP₂= P^*₂P_1+iなので菱形３０面体の辺の部分に四角形をはさんだモノ、また、凧型６０面体のamboとも考えられる。
a+bi=0+3iのとき
a+bi=-1+3iのとき	-1+3i=(1+2i)(1+i)なので、 p-正12面体のjoinもしくは p-菱形３０面体。	-1+3i=(1+2i)(1+i)なので、 p-正12面体のamboもしくは p-正１２面２０面体。
a+bi=2+3iのとき	2+3iはガウスの整数環で素元です。だからこれは他の多面体作用素では書けないと思います。	左の多面体の双対。