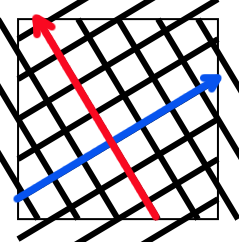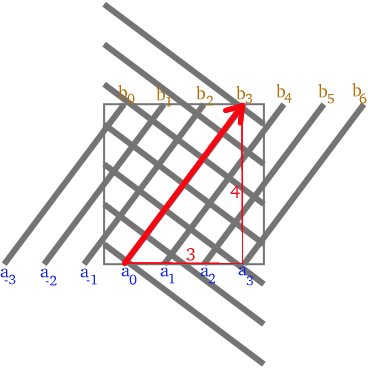
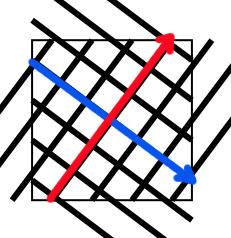
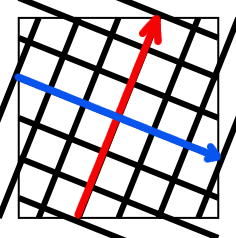
立方体の斜め編み と p-多面体：続き





以下の内容は かなり数学色のつよい内容です。


まずですね。「立方体の（ｋ／ｎ）の斜め編み」と書いていましたが、
いくつかの意味でこの記法はあまり良いものではありませんでした。


そこで つぎのような記法に変えましょう。まずｎは正の整数、
ｋは（−ｎ＜ｋ≦ｎ）の整数とします。（この限定を外しても、定義には問題ないんだけどね。）
面を上から見て、手前の辺の左の端から 右にむかって
辺の長さの ．．．，（−３／２ｎ），（−１／２ｎ），（１／２ｎ）、（３／２ｎ），（５／２ｎ），．．．
すすんだところの点を
．．．，ａ-2、ａ-1、 ａ0、ａ1、ａ2、．．．、として、
同様に向こう側の辺の左の端から
辺の長さの ．．．，（−３／２ｎ），（−１／２ｎ），（１／２ｎ）、（３／２ｎ），（５／２ｎ），．．．
すすんだところの点を
．．．，ｂ-2、ｂ-1、 ｂ0、ｂ1、ｂ2、．．．、とします。
このとき、ａiとｂi+kを結ぶように斜めにつないでいくと、
立方体の表面に斜めに傾いた格子模様を書くことができます。





この格子模様にそって、帯を編むことを （ｋ＋ｎｉ）の斜め編みと呼ぶことにしましょう。（ｉは虚数単位です）




つぎにこの記法を一般化します。
０以外の複素整数ｚ＝（ａ＋ｂｉ）（実部、虚部が整数となる複素数）に対して、
ｚにｉを何回か掛ければ 上の定義が使える複素整数に出来ますから、
その値を用いて複素整数ｚの斜め編みと定義します。
ですので、（−ｋ＋ｎｉ）の斜め編み＝（ｎ＋ｋｉ）の斜め編みです。

図を書いて説明しないと分かりにくいですね。

(3+4i)の斜め編み=(4-3i)の斜め編み (2+5i)の斜め編み=(5-2i)の斜め編み (-3+5i)の斜め編み=(5+3i)の斜め編み

上の図の黒い線が １つの面の上で帯の進む道筋を表します。
模様に斜めに現れる２種類の線分が
その複素数を表すベクトル（を線分と見たもの）になってるわけです。
（帯が出発する辺上のその帯の方向の出発点同士の間隔を１としている。 帯の方向によって、出発点は２種類あるので注意。）

＃斜め編みを示す複素数に虚数単位を掛けても、斜め編みは変化しません。
＃また、０に対応する斜め編みは存在しません。
＃このことは ガウスの整数環Ｚ［ｉ］の乗法に関するモノイドを
＃ｉが生成する部分群 ＜i＞で割った商モノイドＺ［ｉ］×／＜ｉ＞と
＃ 斜め編みが１対１に対応することを示しています
＃↑この説明は難しいから 無視してもいいです。

つぎに 斜め編みと「多面体」との関係を話すために 言葉を用意しましょう。
（ここでいう「多面体」は面のつながり具合いだけを 指定しているので、正確には 「組み合わせ多面体」というんでしょうかね。）
きちんと定義として話すことも出来るんですが、疲れるから 大体で。（ぉぃ）

すなわち、前回 書いたように 斜めに編んだとき、
帯と帯の重なる部分を四角形に見立てて 「多面体」をつくります。
この多面体を斜め編みでできる（組み合わせ）多面体ということにしましょう。



最後に 多面体のp-操作について 書きます。
p-操作のくわしい説明については G.W.Hart氏のページや あそびをせんとやのコラム を見て欲しいのですが、
大体でいうと 多面体の面を切り放して、まわりに四角形をつけたプロペラ状にして、
ひねってくっつけるということです。でも このとき ひねりかたで
右ひねりと左ひねりがあります。つぎの図をご覧下さい。

＃この図を描くのが面倒だった。。 ここでは 左側の方をp-操作、右側の方をp'-操作と呼ぶことにしましょう。

さて、以上で 今回話したいことの準備はすべて整いました。
言いたいことは次の通りです。

立方体の（ａ＋ｂｉ）の斜め編みで出来る多面体にp-操作した多面体は、
立方体の（１＋２ｉ）×（ａ＋ｂｉ）の斜め編みで出来る多面体である。

また、

立方体の（ａ＋ｂｉ）の斜め編みで出来る多面体にp'-操作した多面体は、
立方体の（１−２ｉ）×（ａ＋ｂｉ）の斜め編みで出来る多面体である。



証明は 書きませんが、つぎの図をみればわかるひとには分かるかも。




立方体の１つの面

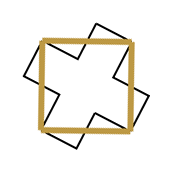面を十字にして隣の面と斜めにつなぐ。
これがp-立方体。

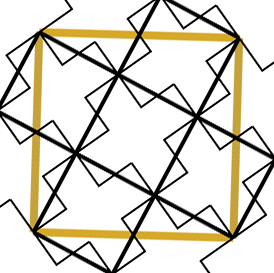小さい面をさらに十字にして隣の面と斜めにつなぐ。
これがpp-立方体。
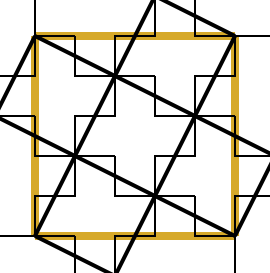小さい面をさらに十字にして隣の面と逆の斜めにつなぐ。
これはp'p-立方体。





この定理を使えば、 立方体は（１＋０ｉ）の斜め編みに対応しますから、 p-立方体は （１＋２ｉ）の斜め編み。
pp-立方体は （１＋２ｉ）２＝（−３＋４ｉ）の斜め編み。
ppp-立方体は（１＋２ｉ）３＝（−１１＋２ｉ）の斜め編み。
pppp-立方体は（１＋２ｉ）４＝（−７ー２４ｉ）の斜め編み。
となります。

＃あそびをせんとやのhhase氏からppp-立方体等の画像を送ってもらいました。
＃上記の結果は 確かに合っています。


さらに、菱形１２面体は（１＋ｉ）の斜め編みで出来る「多面体」でして、 p-菱形１２面体は （１＋ｉ）（１＋２ｉ）＝（−１＋３ｉ）の斜め編み。
pp-菱形１２面体は （１＋ｉ）（１＋２ｉ）2＝（−７＋ｉ）の斜め編み。
ppp-菱形１２面体は （１＋ｉ）（１＋２ｉ）3＝（−９−１３ｉ）の斜め編み。

となるわけなんです。


もどる。