 菱形90面体
菱形90面体

10月4日のあそびをせんとやでも 参照されていますが、
George W.Hart氏のページは 本当にすごいです。
上の画像の形(の表面)は G.W.Hart氏のページ内の
このあたり
に書かれている多面体です。
氏のページ内には このような多面体=zonohedra(面が平行四辺形や、
対辺が平行で長さが等しい偶数角形になる多面体) 及び、zonohedrification
(与えられた多面体から、新たなzonohedronをシステマティックに構成する手法)について、
くわしい解説が載っています。以下、そこで読んだ内容を参考にして、今回の多面体の構成を書いてみます。
平行四辺形を 考えます。平行四辺形の4つの頂点は 2つのベクトルaとbを使うと
原点、ベクトルaの終点、ベクトルbの終点、ベクトルa+bの終点 の4つとなります。
平行四辺形の辺は
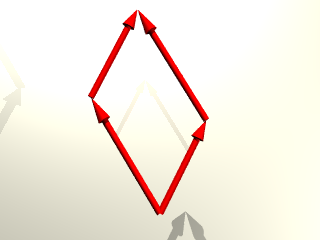
原点とベクトルaの終点を繋ぐ辺
原点とベクトルbの終点を繋ぐ辺
ベクトルaの終点とベクトルa+bの終点を繋ぐ辺
ベクトルbの終点とベクトルa+bの終点を繋ぐ辺
の4つです。
つぎに平行6面体を考えて見ましょう。
平行6面体の8つの頂点は 3つのベクトルa、b、cを使えば、
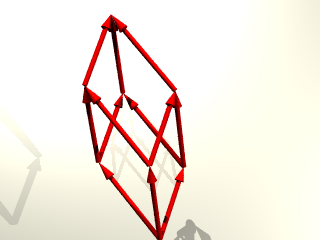
ベクトル0の終点、
ベクトルaの終点、
ベクトルbの終点、
ベクトルcの終点、
ベクトルa+bの終点、
ベクトルb+cの終点、
ベクトルc+aの終点、
ベクトルa+b+cの終点
の8つです。
さて、同様のことを もっと多くのベクトルで 考えたらどうなるでしょう?
たとえば、はじめのベクトルの数を4つにして、つぎの4つのベクトルを考えたら?
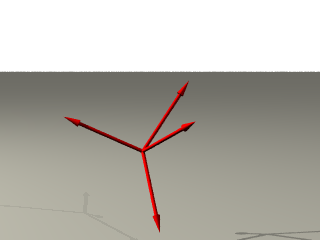
この4つのベクトルをa、b、c、dとして、同様の構成を行うと、つぎの図のように
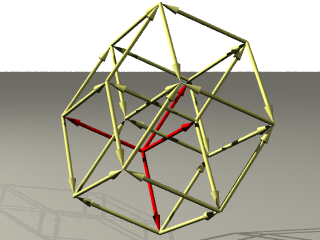
ベクトル0の終点、
ベクトルaの終点、
ベクトルbの終点、
ベクトルcの終点、
ベクトルdの終点、
ベクトルa+bの終点、
ベクトルa+cの終点、
ベクトルa+dの終点、
ベクトルb+cの終点、
ベクトルb+dの終点、
ベクトルc+dの終点、
ベクトルa+b+cの終点、
ベクトルa+b+dの終点、
ベクトルa+c+dの終点、
ベクトルb+c+dの終点、
ベクトルa+b+c+dの終点
の16個の頂点をつないだ形が現れます。
とくに次のような4つのベクトルをつかうと、
(1,1,1)、(1,1、−1)、(1,−1、1)、(−1、1,1)
きれいな形になります。
この形は菱形12面体です。
はじめにつかうベクトルがきれいな対称性を持っていると、
綺麗な形ができあがります。そこで、はじめのベクトルとして、
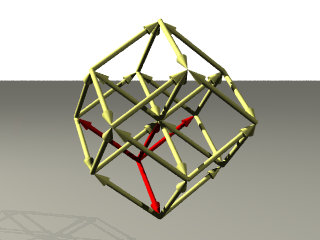
正12面体の10本の対角線のベクトルを使ったのが 今回のトップ画像です。
正12面体の10本の対角線のベクトルとは つぎのような10本のベクトルです。

この10本のベクトルから 上の構成を行うと次のようになるわけです。

 もどる。
もどる。







