Nova Plexusの拡張への道／地の巻＃７
地の巻＃６までをお読みになられた方の中には
もう次に来る物が見えている人も多いかもしれません。
地の巻＃５では 正８面体でしたが、これは正４面体から角を落した形です。
地の巻＃６では 立方８面体でしたが、これは正６面体から角を落した形です。
正１２面体から辺の中点まで角を落した形、１２面２０面体を考えましょう。
| 元の多面体 |
正四面体 | 立方体 | 正１２面体 |
| 角を落すと |
正８面体 | 立方８面体 | １２面２０面体 |
| 辺で出来る中心を通る正多角形 |
３枚の正方形 |
４枚の正６角形 |
６枚の正１０角形 |
| 上記多角形の外側に |
中心を通る３枚の長方形 |
中心を通る４枚の６角形 |
中心を通る６枚の１０角形 |
| フレーム（枠）の初期位置 |
元の正４面体の面の４つの正三角形 |
元の立方体の面の６つの正方形 |
元の正１２面体の面の１２個の正５角形 |
正四面体、立方体、正１２面体はすべて 頂点の次数が３の正多面体です。
次の図のように１２面２０面体の辺からなる正１０角形で
中心を通るものが６つあります。
この正１０角形のまわりに 次のように１０角形をつくります。
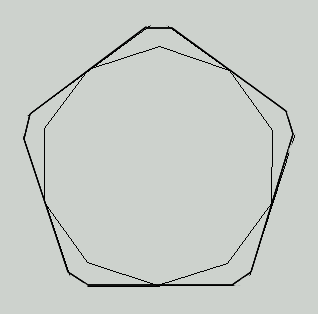
例によってこの１０角形の周の長さを一定にして、
隣り合う辺の長さの比を変化させることを考えます。
また変化の過程の中で、 １０＊６＝６０個の頂点から５個ずつ選んで
１２個の５角形のフレームをつくるのですが、
フレームの頂点は 次の図のように 大きい１２面２０面体の
辺上を動きます。（赤と緑のフレームの頂点の動きを矢印で示す）
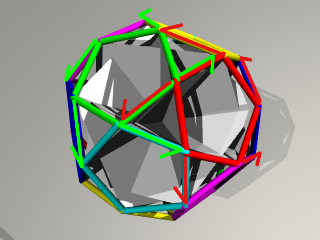
では ＣＧアニメーションを御覧ください。
ＣＧアニメーション(mpgファイル：376kB)
さて、アニメーションを時系列に沿って見てみましょう。
最初の位置は １２面２０面体の正５角形の面です。
このとき 内側には
「あそびをせんとや」で紹介されていた
正５角形を組んだ形が入っています。
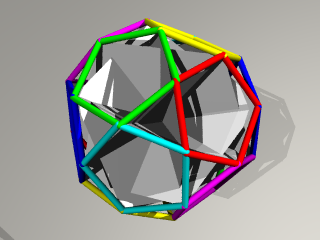
回転しながら 内側に移動していき、
画面中央の正３角形の穴が小さくなります。
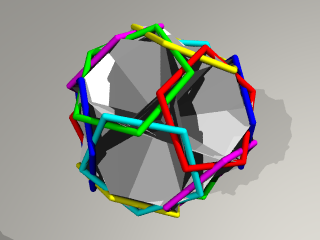（図Ａ）
あるところで ３重点が現れます。
この時 １０角形の隣り合う辺の比はいくつ何だろう？
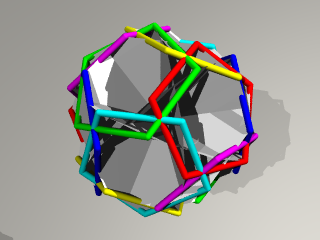
下の図がちょうど辺の比が１：１のところ。
際だった性質は見当たりませんね。
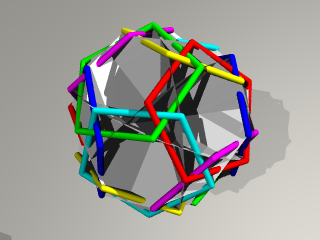
天の巻＃４の３枚目の画像とほぼ同じです。
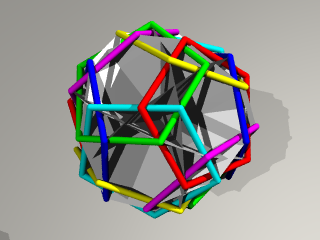（図Ｂ）
そのまま進んで行くと、、、
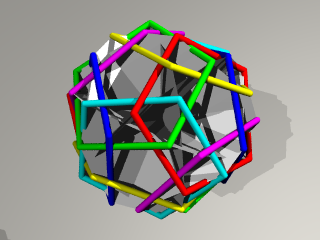
最後はこうなります。
このときも 内側に
正５角形を組んだ形が入っています。
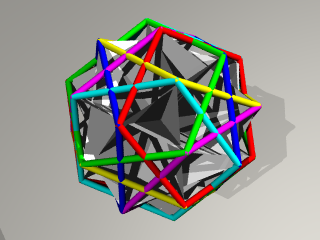
３重点が現れた後の形（図Ｂ）で ５角形を「５すくみ」にしたものが
天の巻＃４での 「Nova Plexusの拡張」でした。
３重点が現れる前の形（図Ａ）もなかなか綺麗です。
ここでは５角形のフレームでしたが、
それは正１２面体の面が５角形だからです。
また、正１２面体の頂点次数が３という事実が、
天の巻＃４での最後の画像の中央付近の小さい正三角形の穴に対応しています。
これが三角形でないと いまひとつ安定しない気がします。
どうしても５角形や四角形よりも 構造としては三角形が安定します。
そういう意味で、正四面体は 各面が三角形で 頂点次数３ですから
NovaPlexusは 安定した形なのでしょう。
（つづく）
もどる。
