Nova Plexusの拡張への道／地の巻＃６



地の巻＃５では、長方形３枚のカードを組んだ形の頂点を繋いで
正三角形を作りました。
以下、１月３１日の「あそびをせんとや」と重なる内容になりますが、
このカード３枚の組み紙は次の図のように
カードの一部を切り取って、正方形の部分だけにすると、 ３枚の正方形の辺が正８面体を形作り、
正８面体の中心を通る３枚の正方形になっています。



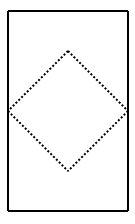
ところで、正８面体は正４面体から辺の中点まで角を落とすことでも、得られます。

正６面体＝立方体から 辺の中点まで角を落すと立方８面体になります。
立方８面体の辺をつなぐと中心を通る４枚の正６角形が得られます。





上記３枚のカードの組み紙で 正方形ではなく長方形で組んだように、
正６角形からつぎのように 外側に６角形をつくります。



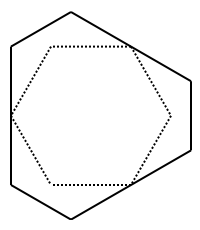
この６角形の周の長さを一定にして、
隣り合う辺の長さの比を １：０から０：１まで変化させることを考えます。

つまり、
正四面体 −＜角落す＞→ 正８面体 → 中心を通る３枚の正方形 → 中心を通る３枚の長方形 →辺の比を変えて動画へ
立方体 −＜角落す＞→ 立方８面体 → 中心を通る４枚の正６角形 → 中心を通る４枚の６角形 →辺の比を変えて動画へ
というアナロジーです。


では 次のＣＧアニメーションを見てください。


ＣＧアニメーション(mpgファイル：234KB)

地の巻＃５での正三角形のフレームの初期位置は
正８面体を 正４面体から角を落したと考える時、
元の四面体の面の残った部分の位置です。

今回の正方形のフレームの初期位置は
立方８面体を立方体から角を落したと考える時、
元の立方体の面の残った部分の位置です。


６角形の辺の比が変化していくとき、
すべての頂点は大きな立方８面体の辺上を動いています。
ですので、今回のアニメーションの正方形のフレームは
立方８面体の辺上を次のように動く４点を結んだものです。




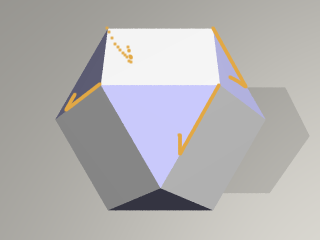
さて、アニメーションを時系列に沿って見てみましょう。

最初の位置は 立方８面体の正方形の面です。




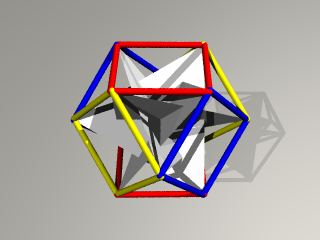
回転しながら 内側に移動していきます。




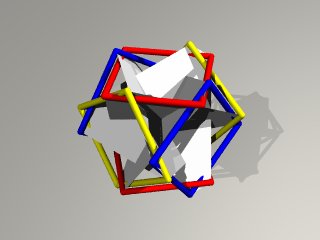
だんだん 中央の三角形の穴が小さくなってきて、、




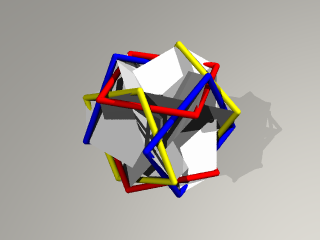
あるところで ３重点が現れます。
この時 ６角形の隣り合う辺の比は１：√２だと思うのですが。。




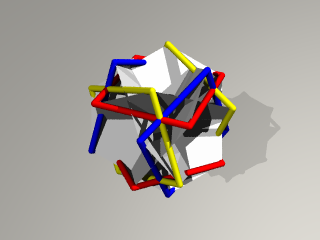
下の図がちょうど辺の比が１：１のところ。
また中央の三角形の穴が大きくなっていきます。




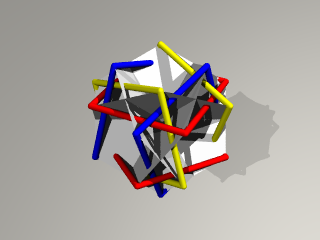
この辺り、天の巻＃１を思い出しますね。




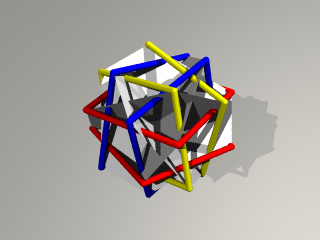
段々、同色のフレームが近付いて来て、正方形の穴が小さくなります。




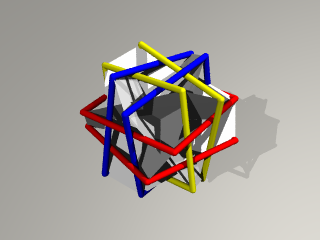
最後はこんな感じ。




（つづく）
もどる。