 複素素数の分布(ガウス整数環の素元分布)
複素素数の分布(ガウス整数環の素元分布)
上の画像、表示がおかしい方は
こちらをお試しください。
Nova Plexusの話ばかりで 疲れたので、閑話休題。
「Nova Plexus拡張への道」は、明日以降の”地の巻”に期待してね。
さて 表題の画像が何を表しているのか説明せねばなるまい。
「素数」という言葉は (数学とあまり関わりの無い人でも)
かなり多くの人に通じる言葉なのではないかと、思う。
小さい方から挙げれば、2,3,5,7,11,....。
さて 2を考えよう。もちろん2は素数だが、複素数まで考えれば、
2=(1+i)(1ーi)
と因数分解できる。
そこで [整数]+[整数]i という形の数のうち、
そのような数まで考えても積に分解できない数を ここでは仮に
「複素素数」と呼ぶことにしよう。
(ちなみに、[整数]+[整数]i という形の数の全体を ガウス整数環と呼ぶ。
ガウス整数環は 素因数分解が一意的に決まる環である。)
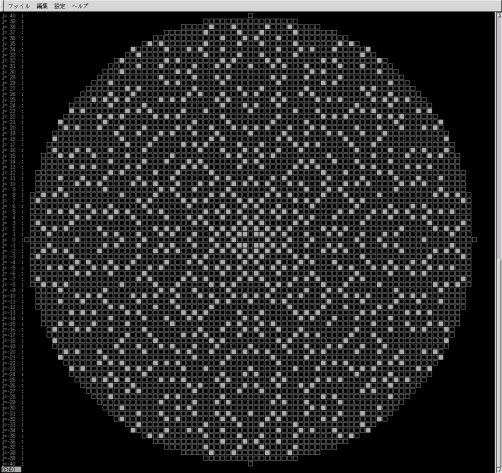
実は 表題の画像は 複素素数の分布を表している。
■が複素素数。
□はそうでない数だ。真中が0。
たまには C言語も使わないと忘れてしまう、、ということで
久しぶりにプログラムを書いてみた。
通常の素数分布では 段々 素数が疎になっていくが、
上の複素素数の画像では 中心から離れてもあまり疎になっていく感じが見えないのが面白い。
この複素素数分布には 想い出深い話がある。
私が大学の学部4年生だったころ、
いつも通り仲のよい友達と学生の溜り場の部屋に集まっていた。
そこに 友人のTがやってきて出したのが この表題の画像と同じもの。
みんなで わぁわぁ言いながら眺めていたものだ。
そのとき、これを眺めていて、私は ふと不思議な事に気付いた。
3と5、それから 11と13のように 差が2の素数の組を双子素数という。
複素素数の分布を 眺めていて、
4つ子素数を考えたらどうか?と思い、そのような組を探してみたのだ。
ここでいう4つ子素数とは、
ある数の上下左右の4つの数が素数になっているもの、つまり、
■
■□■
■
のような部分を探したのである。
上記の□に当たる部分を4つ子素数の中心ということにしよう。
分布を眺めていて、中心の場所を数えてみると、
原点のごく近くの例外を除いて、実部も虚部も5の倍数なのだ。
双子素数というのは結構有名だが、4つ子素数というのは聞いたことがなかった。
仮にあったとしても、それが こんな簡単な性質を持っていることも 意外だった。
その発見を友人に話したところ、意見が割れた。
「をを、ほんとだ!」
「偶然じゃないのか?もっと大きな範囲で調べないと!」
友人Tは
プログラムを修正して、
明日までに もっと大きな範囲で4つ子素数を検索してみる、
と言って、帰っていった。
次の日、学生室にいくと、友人T曰く:
「かなり大きい範囲で 調べたんだけど、昨日の予想 当たっているんだよ!」
「をををを!」
学生室は、にわかに盛り上がり、ギャンブル好きな私はこう提案した。
「1:今後2年間(=修士課程在学中)にこの予想が証明される。
2:今後2年間(=修士課程在学中)に反例が見つかる。
3:今後2年間(=修士課程在学中)では どちらか分からない。
さぁ みんな賭けようじゃないか!笑」
予想の言い出しっぺの私が 「証明される」に賭けたのは言うまでもない。
みんなで 騒いで その日は解散となった。
明くる日、学生室に行くと、また みんなが盛り上がっている。
「どうしたの?」と聞くと、
「あ、濱中!それがさぁ。。。。」
曰く、前日、学生室のメンバーの一人が この予想の話を
京大の吉田教授のところに持って行ったらしいのだ。
そうしたら 吉田先生、「ちょっとまて」といって、考えたのち、
5分ほどで 証明してしまったらしいのだ。笑
さて、ではどうして4つ子素数の中心は[5の倍数]+[5の倍数]iという
形になっているのだろう?
以下の表は 原点(=0)からの距離が300以下の
第一象限内の複素素数a+biが、
aとbをそれぞれ5で割ったあまりについてどう分布しているか、
その個数を計算したものである。
| bを5で割った余りが4 |
529 | 560 | 0 | 0 | 544 |
|---|
| bを5で割った余りが3 |
551 | 0 | 550 | 544 | 0 |
|---|
| bを5で割った余りが2 |
546 | 1 | 540 | 550 | 0 |
|---|
| bを5で割った余りが1 |
557 | 546 | 1 | 0 | 560 |
|---|
| bを5で割った余りが0 |
0 | 557 | 546 | 551 | 529 |
|---|
| aを5で割った余り |
0 | 1 | 2 | 3 | 4 |
この表をみると 個数が0になる部分 つまり5で割った剰余によっては
素元になれない部分が
結構あることがわかる。(証明はしませんが。。)
1個だけというのは原点の近くの例外的な素元である。
4つ子素数の中心になるためには
その中心の回りに4つの素元が配置されなければならないのだから
上の表から4つ子素数の中心になり得る場所を考えてみると
aもbも5で割れないといけないのだ。
 もどる。
もどる。
