サイエンスパートナーシッププログラム事業

サイエンスパートナーシッププログラム事業への参加

平成１４年度サイエンスパートナーシッププログラム（以下 SPP)事業へ参加しました。
今回は県立福崎高校の理数コースの１、２年生３０数名を招いて、「数学入門」というタイトルで計３回のプログラムを実施しました。第１回目松山先生による「整数論への誘い」、第２回目渡辺先生による「三角形の重心は本当に３中線の交点か？」に続いて、第３回目を濱中が担当しました。

濱中担当分：「多角形は切って、組み合わせると必ず正方形にできる？」

前世紀の初め、ヒルベルトは面積という概念の根幹に関わる問題としてつぎの問題を挙げています。

「高さと底面積の等しい三角錐の体積が等しい事を極限操作無しに示せるか？」

ヒルベルトという大数学者の割には、随分卑近な問題だと思いませんか？

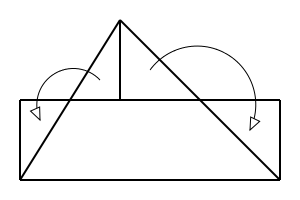
実際、小学校で三角形の面積の求め方を習いますが、
それは三角形を分割して組み合わせ直して長方形にしたりすることによって求めています。
つまり、平面上の多角形の面積を求める際には積分は必要ないことに気づきます。

それどころか
平面上の２つの多角形が等積ならば、
それぞれをパーツに分解し、パーツ毎に合同とすることが出来るのです。

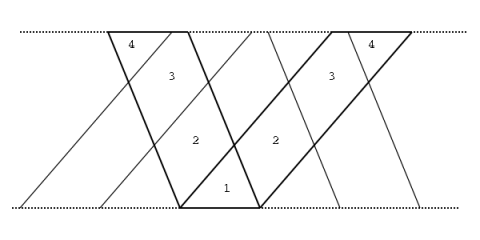
今回のプログラムでは用意した正三角形や正五角形の厚紙を切って繋げて正方形にするという作業をしてもらいました。

正３角形を切って繋げて出来た正方形

ところで、先に挙げたヒルベルトの提唱した問題は結局否定的に解かれました。
つまり、２つの立体は体積が等しくても、
片方を分割して繋げ直して他方に移すことが
出来る時と、出来ないときがあります。

たとえば、どんなときが出来るのでしょう？
実は底面が多角形の柱は必ず立方体にすることができます。
え、想像がつかない？そこで今回はコンピュータグラフィックスを
使って、斜めの三角柱を立方体にするという映像を御覧頂きました。

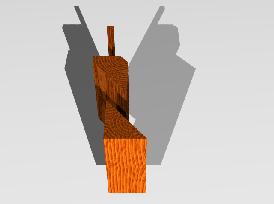
：斜三角柱から立方体への変形を収めたAVIファイル

さて、一方、一般の三角錐は、分割して繋げ直して直方体にすることが絶対に出来ないことが知られています。つまり、平面のときとは違って、三角錐の体積公式を求めるには積分等の極限操作が不可欠なのです。

絶対に出来ないことを証明するにはどうすればいいのでしょう？

「３日、頑張ってみたけど、だめだった。不可能に違いない。」ではだめです。
証明には、なりません。不可能性の証明の方法の１つとして不変量という概念があります。
今回のプログラムでは最後に、不変量の概念を紙と駒を使ったゲームを通して理解してもらいました。

今回のプログラムでは上記の数学の内容をテーマとし、次のような授業、実習を行なった。

平面図形について：初めに、平面図形の面積という概念の基礎的性質を確認したのちに、一般に等積な２つの多角形は分割して繋げ直せば一方から他方に移ることができることを講義した。その後に、それらの一般論を用い、各自工夫することにより、実際に多角形の厚紙（正三角形と正五角形）を切り、繋げなおして正方形にするという演習を通して２次元の特殊性を理解するというプログラムを行なった。

３次元の図形について：一方３次元の図形については、分割して組み合わせることで変形できることと、出来ないことが生じる。可能な変形を説明するには、立体図形の切断、移動が必要で、高度な３次元の空間図形の把握を要し、初学者には困難を伴う。そこで、今回は事前に３次元のCGのアニメーションを大学の計算機を用いて製作し、高校生にそれらの動画をみせながら説明することにした。

不可能証明について：３次元の図形では平面の場合と異なり、分割組み合わせることでは絶対に変形出来ない例がある。実際、「正四面体を分割、組み合わせることで立方体にはできない」。この事実の証明は難解であるので今回の授業では「不可能性の証明」という通常あまり高校におけるカリキュラムには登場しにくい証明の方法論について、「不変量」という概念を説明し、具体的な問題、手で触れるゲームを用いて不変量の概念を体験的に理解できるよう努めた。