ゼミ生：
2005/2/4
ゼミ室の窓から外を眺めると、芸術棟が見えます。
ゼミ室の部屋の窓際に画鋲を１つ刺して、いいました。
「今日は この画鋲からあの芸術棟の屋根の右手前の角までの距離を測ってもらいたい」
「ただし、条件がある。この建物から出てはダメだ。」
「机上の空論はいらない。今すぐ測って欲しい。」
「測るのに必要なものがあれば、できるだけ用意しよう。」
「必要になりそうかなぁ、とおもうものをいくつかこの袋のなかに用意してある。気兼ね無く言いたまえ。」
わいわいがやがや。６人のゼミ生を２つのチームに分け、それぞれのチーム毎に
測り方を考えてもらうことにしました。それぞれのチーム毎に部屋を分かれて
作戦会議開始。
各チーム毎 面白い計測方法がでました。また、それは自然に数学の内容に結び付きました。
学生の思考レベル（良し悪しの意味ではなく）に応じて、中学校数学の相似を使っても出来ますし、
２等辺三角形の性質を使おうとした者もいました。高校の正弦定理を使ってきれいな
計算を示されたときは感心しました。
2005/2/14,18,25このソフトはいわゆるレイトレーシングソフトと言われるもので、
テキストファイルで カメラの位置、視点の方向、光源の位置、物体の形状と位置、
を指定してやると まるで写真を撮るようにコンピュータグラフィックス（CG）として
出力してくれるというものです。とても高機能であるにも関わらず フリーソフトとして
配布されています。
このソフトを使ったことがある人には分かると思うのですが、
このソフトを使うという行為そのものが、もう数学に直結した行為です。
また、立体図形に関する内容の授業をするときには
このソフトで作ったＣＧを図として提示すると
学生がスムーズに理解してくれることが多く、授業でもよく使っています。
ただ、すべての物体の位置は３次元座標で直接与えないといけないので、
思い通りの画像を作ろうとおもうと 計算、計算、計算。
ですが、計算という行為が、机上の計算で終わらず、画像として出力されると
大変モチベーションが違います。実際、今回のゼミでも pov-rayの楽しさに
のめり込む学生がおりました。
座標計算して物体を作って それがCGとしてきれいに出力される感覚。
やらないと分かってもらえないですね。楽しいんですよ。まじで。
まず最初の２回は pov-rayの使い方、シーンファイルの書き方を教えました。
そのうえで３回目のゼミでは ちょっと応用的なことに取り組みました。
「今日もみんなノートパソコン持ってきた？はいはいOK。」
「では、今日は pov-rayで 作ってもらいたいものがある。」
「今日は このゼミ室を作ってください。」
「全員で共通の座標を使えば、各自自分の担当する物体だけ作って最後に組み合わせることができるだろ。」
「まず、この部屋のここの隅を原点にしよう。そんでこっち方向がｘ座標ね。」
「１ｍを １単位とするからね。みんなは 今決めた座標空間の中にいるんだ。」
「とりあえず、みんなこの部屋のいろんな場所の長さ測って、設計図書こう。」
わいわいがやがや。
黒板に部屋の見取り図を書いて、あちこち長さを書き入れていく。
「じゃぁ、各自 自分の作りたいものを作りたまえ。」
テーブルを作る者。部屋の隅の柱をつくる者。黒板を作る者。窓を作る者。椅子を作る者。
さすがに椅子は かなり形状が複雑なので、その場では完成しませんでしたが、
大体の部屋の様子は完成しました。また、椅子を担当した学生は 春休みをかけて 椅子を
完成させ、学期明けにデータを持ってきました。かなり 美しいゼミ室のＣＧが完成しました。
ご覧あれ。
クリックすると大きくなります
2005/4/12黒板に自然棟の１Fの図を描いて、１ヶ所に黄色いチョークで印をつけました。
「ここに何があるか、分かる？」
学生たちはあまり覚えていない様子。
「実は、この場所にはね。車椅子の人にも使えるようになっているトイレがあるんだよ。」
「このトイレのドアが実に、面白くてね。数学の香りがプンプンするのだ。」
「ということで、今日はこのトイレのドアについて調べ、それを発表してほしい。」
例によって、６人のゼミ生を３人ずつのチームに分け、チーム毎に調べてもらいました。
彼らは 直ちに ５階のゼミ室から １階へと降りていきました。
ただ、調べろと言われただけなのだから、具体的にどういうことを考えるのか、も
自分で考えなければなりません。教科書にあるように ＊＊は＊＊ですか？＊＊はどうなっていますか？
のような問題ではないのです。
こういう行為は 多分に 数学的センスを要求されます。
また、ドアの機構という、動きのあるものをいくらじっと眺めていても、
何も分かりません。調査、研究と言ったら大げさですが、こういう調べるという行為、行動を
どう開始していいか分からない学生もきっといると思うのです。
実際、「数学的に調べる」という行動をどう起こしていいのか分からずにいる学生も見受けられました。
ドアは以下の写真のようになっています。
上の写真は外からみた概観。すきまから上を見上げると、次のようになっています。
彼らが調査した結果、写真のABの距離とBCの距離は等しいようです。
足下をみたところ。
内側から見たところ
まずは この現実の機構を何らかの方法で 数学的にモデル化する必要があります。
何が動かない点で、何が動く点なのか。それらの点の間にどういう拘束条件があるか。
それを把握したあと、一方のチームは 次の写真のように 動きを紙面上で作図してみました。
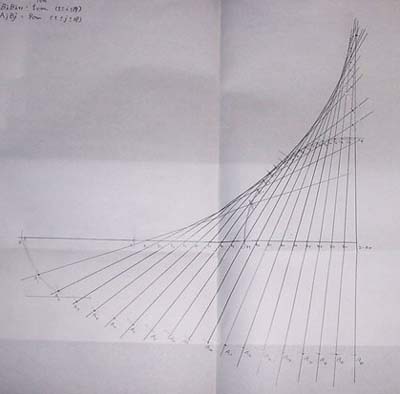
やはり、どうしてもここでドアの左端の動く曲線状の軌跡に目が留ります。
しかし、そこに着目してしまうと、それ以上なかなか計算が進みません。
そこで、「ドアの右端の点がどう動くのかをかんがえてごらん」と示唆してみました。
さて、ドアの右端の点はどのように動くのでしょうか？
これは中学校の数学の範囲です。
それを踏まえて、ドアの左端の点はどのような軌跡を描くのでしょうか？
これは高校の数学の範囲です。
では、上記の写真でＡＢ≠ＢＣだったら どうなるのでしょう？
どうも、この場合は４次曲線が現れるようで、かなり難しくなってしまいます。
＃このことは 後から気付いた。
シンデレラで作ったアプレットを
こちらに置いておきます。
2005/4/19敢えて多くは語られていないようなのですが、私にとってはどれもとても刺激的でした。
どうも学部生にしても、院生にしても、受験の呪縛から逃れられていないのか、
すべてが明示された「問題」を解くことばかり考えていて、
おおまかな「問題意識」だけを提示されただけでは、前へ進めない様子をよく見掛けます。
そこで、この回では、そちらのページで紹介されていたものの一つ、「車の内輪差」
について扱ってみました。
2005/4/26この回は、教員採用試験対策として、集団討論をしました。
ゼミの集団討論としては初回である今回は基本的なテーマですが、
「教員に求められる資質について」というテーマにしました。
いきなり集団討論を行なわせるのではなく、あらかじめ１週間前にテーマを提示して、
小論文を提出してもらい、その上で集団討論をしてもらいました。
2005/5/10数学的題材を独自の視点で アトラクティブに紹介してくれていて、とても面白いサイトです。
今回は 2004/3/23にそちらのサイトで紹介されていた話題をもとに 学生に紹介してみました。
まずは
「電卓に好きな数をいれ、「×」、「５」、「＝」、「√」、「√」 の５つのボタンを
この順に押すことを繰り返してみると、どうなる？出てきた値は何だろう？」
という出題をして、様子をみました。
「なんか 収束してるよな、これ。」
「ちょっと 最初の方の数を式で書いてみようぜ。」
今日は順調なすべりだし。
得られる収束値が ５の３乗根であることに ちゃんと気付いてもらえました。
実際に、その得られた数（近似値ですが）を３乗してみると、たしかに
５にとても近い値になります。
つぎに、黒板に
「では ５の７乗根の近似値の求め方を考えよ」
とだけ書いて また紅茶を入れに行きました。
数分たって様子をみると、どうもすぐに気付いたようです。
「ってことは、２nー１乗根は 計算できるってことかぁ。」
なんて言葉も漏れていて教えてる方としても うれしくなります。そこで、次は
「じゃぁ、５の５乗根の近似値の求め方を考えよ」
と書いて、また様子をみました。今回は ちょっと長めに悩んでいました。
実際、いくつかの手法があります。そのうちに、Ｈ君が
「３乗根、７乗根、１５乗根、３１乗根は計算できるんだよな。。。。あ。」
と気付いて何やら計算を始めました。彼の計算方法（を簡略化すると）は
「一度１５乗根を求めて、それを３乗すれば、５乗根になる」というもの。
彼の発表の寸前に気付いた Ｄさんもちょっと悔しそう。
私「なるほどー。でもね、指数法則によれば、
１５乗根を３乗するのではなく、３乗してから１５乗根でもいいんだよ。」
学生「あっ」
私「だから、単に１２５の１５乗根を求めればいいのだ」
その後、この計算方法と２進数の関係、別の５乗根の計算方法、
また、グラフをつかった収束の様子や原理、の説明等をしました。