過去の表紙31

立方体状の捻れたフレーム

過去の表紙30で紹介したフレーム状のＣＧで、
フレームの太さを一気に太くしてみると以下のようになります。
この造形を題材に簡単な群論を展開してみましょう。

6本のループがありますから 6色で塗り分けてみましょう。

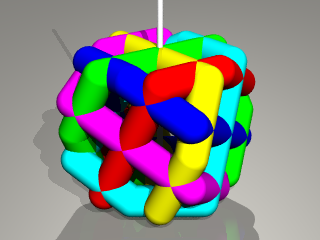
これを6色よりも少ない色で「綺麗に」塗り分けることを考えたい。

まずはじめに、６つのループは互いに「対称な位置にある」と言えるでしょうか？
もちろん、「任意の色のループを任意の別の色のループへ移すことが可能」
という意味では対称といえます。

さて、上の図の手前の角ではR(=赤）、Y(=黄）、B（=青）の3色が集まっています。
反対側からみるとどうなっているでしょう？
白い軸にそって180度回した、「裏側の映像」は次の通りです。

この裏側の映像をみると、ちょうど反対側の角でもRYBが集まっていますね。
つまり角は８つありますが、「角での3色の集まり方」は４通りしかないことになります。

このことから考えて、６つの色のうち、「角に集まる3色」と「角に集まることのない3色」がある
ことになりますから、６つの色の間に完全な対称性があるとは言えなさそうです。

（鏡映を含めた）立方体の自己同型は
立方体の4本の対角線の入れ替えと完全に1対1に対応し、
４次対称群と同型になります。
立方体の自己同型により、4本の対角線を好きに入れ替えることが出来るということですから、
その意味で4本の対角線は「完全に対称」といえるでしょう。

立方体の位置を入れ替えると（自己同型で動かすと）
6色のループも入れ替わります。
つまり４次対称群（対角線の入れ替え）から６次対称群（6本のループの入れ替え）への
準同型（単射準同型）が現れます。

さて6色のループを２つのグループへ分類することを考えます。
このとき、立方体のすべて自己同型が、「6つのループの２つのグループへの分類」を保つように
2つにグループわけすることが出来るでしょうか？
もしそのような色分けがあるとすると、立方体のすべての自己同型がその色分けを保つのですから、
立方体の構造がアプリオリに持つ色分けということができるでしょう。
ところが答は否です。

では 6色のループを３つのグループへ分類することを考えましょう。
立方体のすべて自己同型が、その分類をを保つように、３つにグループわけすることが出来るでしょうか？
今度は「然り」です。

それが以下に示す画像です。立方体を入れ替えるとき、同色はかならず同色に移ることが見て取れるでしょう。

この3色への分類により、
立方体の自己同型＝4次対称群が 3色の入れ替え＝３次対称群を引き起こします。
つまり 4次対称群から3次対称群への（全射の）準同型が引き起こされます。

この準同型の核は何でしょう？

4次対称群の位数（＝元の個数）が２４、３次対称群の位数が６ですから、
準同型の核は位数４ですね。群論を知る者には答は想像に難くないでしょう。
準同型の核は 2次2面体群D₂＝Z₂＋Z₂です。