cubic lattice knot(figure 8 knot)




８の字結び目(figure 8 knot)とは 次のような結び目です。


いわゆる三葉結び目が 最小交点数が最も小さく、
最小交点数が３である（鏡映を除いて）唯一の結び目で、
まぁ （非自明なもののうち）一番 簡単な結び目です。

そして、８の字結び目は 最小交点数４である唯一の結び目なわけで、
そのつぎに簡単な結び目といえます。
まぁ 有名どころの結び目です。


３次元のCGで書くと ８の字結び目はこんなの↓


いつも拝見させて頂いている「 あそびをせんとや 」のページの
バナーに載っている図形は 三葉結び目を 角材で実現した形です。

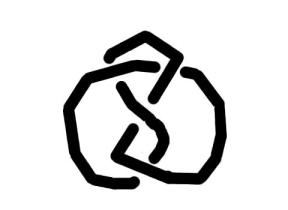
そこで ８の字結び目を同様に実現する形で、
なるべく綺麗なものがないか、と考えたのがトップに載せた形です。

８の字結び目と同値になっていることが 分かりますか？

この形、つぎのように色分けすると 平な渦巻状の部分が２個と、
それらをつなぐＬ字型の部分が２個で出来ています。


なるべく 対称性がある様に、
また なるべく曲がる回数が少ないように等を意識してつくりました。

さて これらを考えるうちに ふと 思った問題があります。

３次元空間内で 三葉結び目や ８の字結び目を
x,y,z軸のいずれかに並行な折れ線だけで実現するとき、
折れ曲がる回数の最小数はいくつでしょうか？

そこで、ちょっと論文を検索してみました。
すると 次のような論文がみつかりました。

E.J.Janse van Rensburg & S.D.Promislow ／ "The Curvature of Lattice Knots"
Journal of Knot Theory and Its Ramifications Vol.8, No.4 (1999)


思ったよりも 結構最近の論文ですね。

さて、ｘ，ｙ，ｚ軸に並行で長さが自然数の線分をつなげた折れ線だけで
できた結び目をcubic lattice knot などと呼ぶようです。
このとき 折れ曲がる回数は cubic lattice knot の曲率と呼ばれます。
（正確には折れ曲がる回数にπ/2をかけたものだけど、
便宜上 回数のことを曲率と呼ぶことにしましょう）

上記の論文によれば

結び目Ｋを実現するcubic lattice knot の最小曲率は、 [Ｋの橋指数]の６倍以上である

その他 Ｋを表すコードを用いた組み合わせ的な論法で得られた結果が
載っていますが、最小曲率の下からの良い評価は得られていないようです。

たとえば 三葉結び目は 橋指数が２なので cubic lattice knotでの最小曲率は１２以上。
hhaseさんの「 あそびをせんとや 」のバナーで 曲り角１２なので
１２が最小であることが分かります。

しかし ８の字結び目も 橋指数が２なので
同じく 最小曲率が１２以上であることは分かりますが
このページのトップにある物の曲がり角の数＝１４箇所よりも少ない実現は
見つかっていない（おそらく 無いのでは。。）とのことです。