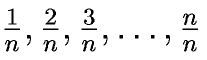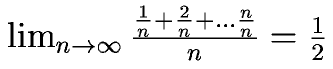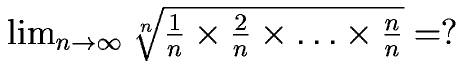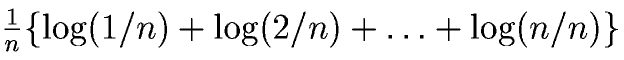200511

2005年11月の低次元日記

05.11.08 人口

兵庫県は三田市というところに住んでいるのですが、
三田市の市役所のページをみていた妻が、「あれ、不思議！？」と。

なになに？と聞くと彼女曰く
「三田市の市役所のページによると、男性人口も女性人口も減少していて、
当然総人口も減少しているんだけど、」

ふむふむ

「世帯数は増えてる」

？！

さて、どういう状況でしょうか？想像してみてください。

05.11.10 病気と確率

ときどき、大学の談話室にある数学教育の論文雑誌をぺらぺらとめくります。
そのなかに書いてあった問題を少々アレンジして紹介します。
　　　岩崎浩「中学校確率の発展的教材としての条件付確率
　　　--面白い問題を中心としたその発展課程の再構成--」上越数学教育研究 20号より

1000人に１人という珍しい病気ですが、発見が遅れると死に到るという恐ろしい病気、
ほげほげ病がありました。そこでこの病気にかかっているかどうかを早期に発見する
検査方法が開発されました。
まず、ほげほげ病にかかっている人がこの検査を受けると９８％の確率で陽性反応がでます。
また、ほげほげ病にかかってない人がこの検査を受けると１０％の確率で陽性反応がでます。
いま、あなたがこの検査を受けたところ陽性反応がでてしまいました。
あなたはどの程度心配するべきでしょうか？
つまり、あなたが病気にかかっている確率はどれくらいでしょうか？

こうしてみてみると、医学や生物学など確定的ではない実験、調査を行なう分野では
条件付確率って必須の修得単元ですね。

05.11.15 携帯電話

先日、某パズルの会に行った帰りの電車で、
あわてて阪急電車の車両に乗ったら最後尾の車両でした。
で、窓には
「先頭車両と最後尾は携帯電話の電源OFFの車両なので、ご協力下さい」
という内容の張り紙があちこちに貼ってありました。

まぁ、どの車両に行っても混んでいそうで、座れそうもなかったので、
携帯電源をOFFにしました。

と、前をみると堂々と携帯電話でメールを書いている女性がいました。
近寄って「ここは携帯電話の電源OFFの車両ですよ」というと、
慌てて隠そうとするので、
「違います。電源OFFの車両です」
と言ったら電源をOFFにしていました。

と、もとの場所にもどり、書籍や入手物に目を通そうかな、と思ったら、
別の場所でも携帯電話を操作している女性。、、と反対側にも。。
やや、おじさんまで。。

もう注意する気が失せました。ふぅ。

私の伯母はペースメーカーを使用しています。
最近、外に出るのは恐怖を伴うようです。

と、ここで考えたのですが、今度無地のTシャツに大きく、
「私はペースメーカーを使用しています」とプリントして
電源オフ車両の電車に乗ってみたら面白いかも。
そんでもって、携帯電話の着信音がなったら倒れたフリをするのだ。
うわははは。ってシャレにならないか。

平均値

今日、数学セミナー(2005/11月号)の「エレガントな解答を求む」のコーナーを
読んでいて、懐かしい問題を思い出しました。

高校生の頃に考えた話。ｎを自然数とします。このとき、次のｎ個の分数

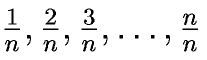
の平均を考えます。もちろん、普通に相加平均を考えると、だいたい１／２になります。
特にｎ→∞の極限値を考えれば相加平均は１／２に収束します。

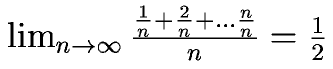
さてでは、ｎ→∞とするとき、相乗平均はいくつに収束するでしょうか？

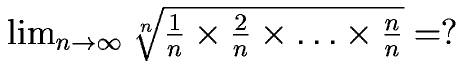
この極限の式のlogをとり、積の形を和の形にすると、

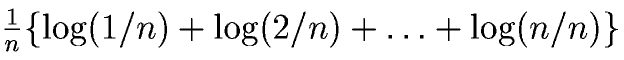
となり、これは次の積分の区分求積法だ、と考えました。

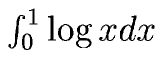
でもこれは異常積分になってしまいます。でも、高校生だったので
そんなことお構い無しに、計算を続けました。

上の積分の絶対値は次の図の青い部分の面積だ。
（この積分では積分する関数が積分範囲で有界でないのでその当時は何か心配でした。）

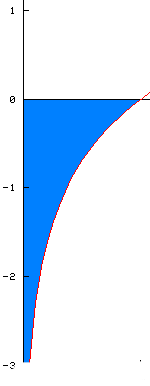
だから、この図を90度回転させて次のオレンジ色の面積を計算してもいいだろう。

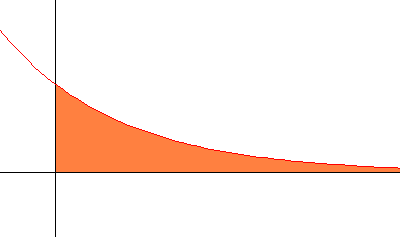
（これなら、積分区間が有界でなくなるけど、積分する関数は積分範囲では有界になるので、
ちょっと安心でした。笑）これを計算すると、

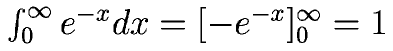
この結果をつかうと青い部分の面積も１。だから、その上の積分はー１で、
だから、つまり相乗平均は１／ｅに収束するのだ、、、と
この得られた結果がとても美しいものに見えて、大変嬉しかったのを記憶しています。

ところが、この計算をその当時の先生に話したらそれは異常積分だからそれでは
正しい証明とは言えない、実際に成り立つのかどうかはとても微妙である、と言われて
とてもがっかりした記憶があります。
今、見返してみると、確かにめちゃくちゃ強引な方法ですよね。笑
＃異常積分であっても区分求積法はそのまま使っていいのかな。

さて、それでですね。今回のエレガントな解答を求むの問題で証明を要請されている
不等式、ちょっと変形すると、この相乗平均を決定する式になるんですよ。
そうかぁ、こうやって証明すればいいのかぁ！と膝を打ちました。
小問２つになっていて誘導のある問題なのですが、その誘導がとてもエレガントです。
大変、面白く解きました。

05.11.24 機内案内

先日、出張で飛行機に乗りました。
飛行機に乗った際、機内の音楽サービスがありますよね。
ちょっと変ったイヤホンで、あれって長時間聞いていると結構
耳が疲れるんですけどね。で、よくその機内放送を利用します。
ところが、あれを聞いている最中に、機内案内で中断されることがあります。

「ポーン、、只今シートベルト着用のサインが点灯致しました、、、云々」

これ、何とかしてほしいと前々から思っていたのです。

いやね、私だって音楽を聞いているのが中断されるくらいのことなら、
いちいち文句なんかいいませんよ。なにより安全のためのアナウンス
なのですから。

でも、でもね。私は落語を聞いているのですよ！
（機内放送のチャンネルのひとつに必ず落語チャンネルがありますよね。
あれ、大好きなんです。）それなのに、、さぁ、話の山場という部分、、
はたまた、さぁどうオチがつくのかな？！という瞬間に

「ポーン、、、ただいまから機内販売を開始致します。云々。」

ぐぁぁ、はやくアナウンス終わってくれ、、、、
ところがこのアナウンス、、意外に長いんですよね。
そんでもって、

「、、、、ありがとうございました（アナウンス終わり）」

と思ったらもう次の落語に入ってた暁にゃ、もうやんなってしまいます。
せめて、アナウンスの最中は機内放送をmuteするのではなくて、
一時停止にしておいてくれ！！と前々から思っておりました。

ところが、今回のフライトで、同じ落語を二度聞いたので気付いたのですが、
今回のフライトではアナウンスの際に、機内放送を一時停止してくれている
ようなのです。すばらしい！！これで安心して機内放送が聞けます。
とてもうれしいです。よかったよかった。

対角線の長さ

2005年11月21日のあそびをせんとやの記事のなかで、
正7角形の対角線の長さに関する関係式の話が紹介されています。
それをみて思い出した話を書いておきます。

単位円に内接する正ｎ角形を考えます。この正ｎ角形の１つの頂点Aから
他の頂点(n-1個ある)までの距離をすべて掛け算するといくつになるでしょうか？

急には分からない？ではn=4のときは？n=3のときは？n=6のときは？予想がたちましたか？ほんとにその予想はあっているのでしょうか？
これ、どこで読んだんだっけ？とても美しい結果だと思います。

証明は複素平面を用いると簡単で、そういう意味でも教育的です。

05.11.29 相似分割

匹見で行なわれたパズルの会へいった折にでた話で、
以下のような問題がありました。（出題者の小松さんに了承を得てここに解説します。）

平面図形Ｆを２つの領域Ａ，Ｂへ分割する際にＡとＢが相似であるとき、この分割を相似分割といいます。場合によっては複数通りの相似分割を持つ図形があります。ではなるべく多くの相似比で相似分割できるような図形を探してください。

パズルの会の開催中に運よく 3種類の相似比の相似分割をもつ図形を思いつくことができました。

なに、気付いてしまえばなんてことはない図形です。それがこれ。↓

つまり、図形そのものは長方形なんですね。長方形の比率は１０：２１です。
左から順に相似比１、 1.37（近似値）、２です。

ところで、この発想でもっと多くの相似比の相似分割をもつようにできないか？
できるんですね。というか、実は正方形以外の長方形はどれもこれも、可算無限種類の
相似比で相似分割できるのです！

もうすこし詳しく述べましょう。上記の長方形の相似分割をみれば、
階段状の段数を多くすればいいのでは？とおもうでしょう。はい。

実際、もう1段おおくしたのがこれです。

相似比をxとすると、各部の値は右のようになりますから、
長方形の縦横比は(1+x²+x⁴+x⁶)：(x+x³+x⁵) になります。

つまり、縦横比ｒの長方形に対して、

ｒ＝(1+x^2)/x
ｒ＝(1+x^2+x^4)/(x+x^3)
ｒ＝(1+x^2+x^4+x^6)/(x+x^3+x^5)
ｒ＝(1+x^2+x^4+x^6+x^8)/(x+x^3+x^5+x^7)
‥‥
‥‥

のそれぞれの式に解があれば（それらの解が全て異なることは証明できるので）
それぞれが長方形の相似分割の相似比になります。

さて、上の式の右辺の関数のグラフを描いてみると次のようになります。

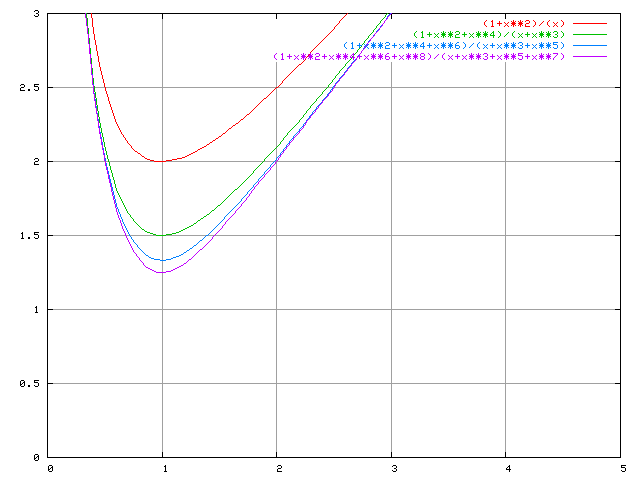
段数の多い相似比の関数になるほど、下側になっています。
また最小値はそれぞれ、２、3/2、4/3、5/4、、、となっていて、１に収束します。

つまり１より大きいｒに対してはｙ＝ｒとの交点が可算無限個になりますから、
正方形でない長方形に対しては無限通りの相似比で相似分割できることになります。

また、特に２より大きい縦横比の長方形の場合は任意の段数で相似分割することができます。

上のほうで図示したのは縦横比２.１の場合という訳です。

日記トップへ