2005年02月の低次元日記
05.02.02
IRC
今日、久しぶりにIRC(インタネットリレーチャット=インターネットを利用した
標準的チャットサービスのこと)にはいって、何の気なしに
#math というチャンネルに入ったら、そこにいたとあるユーザーから
(英語ですが)
「Sがユークリッド空間の凸集合であるとき、
Sの境界と Sの閉包の境界が等しいことを示せ」って誰か分からない?
と聞かれました。ちょっとお酒が入っていることもあって、
数分悩んでしまいました。なかなか 面白い問題だと思うのだけど
どう?>これを読んだ数学関係の人
05.02.07
縁
ま、与太話というか、妄想話ですけども。
アニメの方はともかく、原作を読むと、「攻殻機動隊」という作品のなかには
縁という言葉がよくでてきます。「攻殻〜」に限らず、史郎正宗の作品には
よく出てくる言葉のようですけども。
そこにでてくるのは、一度関わった人間と人間、いや モノでさえ、何かの縁故の発端があれば、
それはいつまでもつづくものであり、それぞれの存在自体に組み込まれていく。
また、深い縁が出来た者同士は 互いの存在が相反したり、同調したりする、
という考え方。
今日、量子力学の特集を読んでいて それを思い出しました。
量子力学にエンタングルメントというのがあるのだけども、考えてみると
このエンタングルメントという量子状態と、縁という概念はとても似かよっているのです。
例えば、2つの粒子A、B がそれぞれ+とーの状態を取りうるとしよう。
つまり 可能性としては (A,B)が (+、+)、(+、ー)、(ー、+)、(ー、ー)の
4つの状態を取り得るのだけども、このうち (+、ー)(ー、+)の状態しか取り得なく
なったとき、この2つの粒子の系はエンタングルメントの状態にあるといいます。
(もちろん、これはエンタングルメントの一例ですが)
量子力学のお約束だが、それぞれの粒子は+やーの状態の混在状態にある。
ちょうど 人間の意識が ロボットのそれとは違って常に揺れ動いているかのごとく。
この2つの粒子のうちのAの粒子を 遠く離れた星まで持っていく。
その星で 何らかの原因で 粒子Aの量子状態が崩壊すると、
どんなに粒子Bが遠く離れていても、粒子Bにも量子状態の崩壊が起こる
ということが量子力学の結果として知られています。
今のたとえで言えば、粒子Aが揺らぎの混在状態から+の状態に収束すれば、
かならず粒子Bは揺らぎの混在状態からーの状態へ収束しなければならないのです。
生命というこのゆらぎの多い存在は 何らかの量子状態を根元としているのかも。
生命と生命の関わりのなかで 多くの縁=エンタングルメントが発生しているのかも。
05.02.08
Top画像
今日、ちょっと思いついたことがあって 昼間にそのアイデアをTop画像にしてみたのだけども
夕方に家に帰って見返してみると 想定してなかった別解に気付きました。
しかも、その別解の方が 面白いじゃないか。
そこで、その別解のアイデアを使ってトップ画像を作り直しました。
うん、こっちのほうが 美しいし、面白いや。
05.02.09
645
今日、通勤の帰り道、信号で止った際、前にいた原付のナンバーが
「・645」でした。
条件反射で、「大化の改新」だ、、と思いました。
教育の威力って凄い。
確率
よくある確率の問題で、
「双子が産れる場合、男の子と女の子が一人ずつ産れる確率を求めよ」
というのがあります。もう ほんとに、話題にするほどのこともないくらいに、
あまりにありふれた「よくある」数学の問題ですけども、
この問題を真剣に考える今日この頃です。笑
05.02.14
球面の裏返し
うちの研究室の公式の方のページの下の方に
球面の裏返しの途中の状態の模型の写真を載せています。
球面が自分自身と交差することができるとして、なめらかなままに 裏返すことができるか?
という 数学関係では 有名な話ですけども、数年前に図書館に所蔵されているその裏返しの映像を
ビデオで見たことがあります。ふと、もう一度それがみたくなったのですが、
いまの技術なら どこかにもっと きれいなCGがあるんじゃないだろうか?と
webを探したら ありました。とてもきれい。おすすめです。
こちらのサイトの
ここに
realaudio形式のファイルが、
ここらへんにquicktimeのファイルがあります。
05.02.15
折り鶴とグラフと多面体の関係
詳しくは書かないけど、今日気付いたこと。
与えられた多面体に対して、その多面体と同じ組合わせ構造を持つ多面体のなかにもっとも「自然な形」
が合同を除いて一つ存在することが知られています。
これは その多面体のグラフとその双対グラフを平面上に同時コイングラフ表示することと関係します。
変形折り鶴のうち、首尾と翼が交換可能な折り鶴は
四角錐のグラフ及び双対グラフの同時コイングラフ表示に対応するんだな。。
ふむふむ、なるほど。
理系と文系
学問として、理系と文系の思考方法は実は同じであると思う。
それらの間の違いは探求方法の違いなのである。
探求方法の違いは それぞれの学問の求めるところの違いによる。
つまり、事実の探求と、考え方の探求の違いである。
ということは それらの違いは 探求者でなければ現れないということである。
探求せぬ者の間では なるほど、理系 文系の違いが誤って理解されたり、
別の意味として 分類されたりすることもうなずけることである。
例えば 嗜好の違いによる文系理系の別である。これは探求にまだ足を
踏み入れておらぬ者が自分の興味のある方向をもってして自分の方向を定めることであり、
無理からぬことといえよう。
もうひとつは 社会的意味での理系文系である。つまり、受験や就職とからめて
自分自身を文系理系に色分けすることが社会的に要求されることにより、
何らかの意味で文系理系の別を自分自身に課してしまうわけである。
この端的な間違いの1つが 数学が苦手=文系の思考方法である。
この最後に述べた思考が 一般に流布しすぎているために、文系=成績がよくない というような
ゆるやかなイメージがあるのではないだろうか?もちろん、文系でも抜群に頭の
よい人がいることは 誰でも知っていることである。
理系離れがさけばれて久しいが、実は理系が敬遠されているというより、
文系が軽視され、低く見られかねないことのほうが問題なのではないだろうか、
と思う今日この頃である。いずれにせよ、文系理系を問わず単に若い生徒たちの間で
全体的な学問の地盤沈下がおこっているのかもしれない。
05.02.17
四角い穴
ルーローの三角形っていうのは 次の図のような図形で、
どちらの方向から測っても 「幅」が同じとなる定幅図形としてよく知られています。
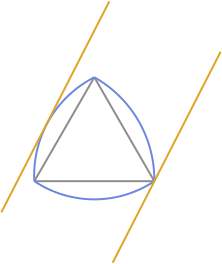
定幅なので この図形は正方形の内部で回転することができます。
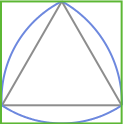
さて、ルーローの三角形の性質をうまく使って 四角い穴を開けるドリルがあるらしい、
という話も結構 有名なんじゃないかな、と思うのですが、実物をみたことはありませんでした。
はて、ネットで探せば 実物の写真があるかな、と思い ちょっと検索したら、
一件だけ見つかりました。
http://www.integerspin.co.uk/polygon.htm
リンク先のサイトの方もカタログで見ただけで 実物は見てないようです。
実物、いまでもどこかで売られているんでしょうか?
追伸:現在 木材に四角い穴を開ける道具としては「角のみ」というものがあるようで、
これは ルーローの三角形とは関係ないんですね。しかも、ルーローの三角形を使ったドリルよりも
使い勝手が良さそう。(って どちらも触ったことはないのですが)
なので、いまさら 四角い穴を開けるドリルは需要がほとんど無いのかも知れません。
05.02.18
conscious
最近、通勤中にFMをよく聴くのですけども、そこでエコ運動の啓蒙CMが流れていて
「はじめよう アースコンシャス(earth conscious)」
と言っていました。
「コンシャスって 聞いたら、 ボディコンを思い出して 意味わかんない人多いんじゃないかな」
とかみさんに言うと「ボディコンなんか思い出さん」と言われてしまいました。
年代の差かな。
ちなみに、consciousは 「**を意識した」という意味の形容詞です。
earth consciousは 地球のことを考えた(生活)、
body consciousは 体型を意識した(ファッション)、
という意味ですね。
05.02.28
問題
今日、W先生から聞いて、気になり出して止らなかった問題。
3つの自然数の組(a,b,c)と(d、e,f)で
a+b+c=d+e+f、 abc=def
となるものって どれくらいあるんでしょうか?
もし、そのような(a,b,c)と(d,e,f)があれば
3辺の長さが(b+c)、(a+c)、(a+b)の三角形と
(e+f)、(d+f)、(d+e)の三角形を書くと、
これらの三角形は周の長さと面積が共に等しくなります。
しばらく悩んでしまいましたが、こうしたらどうでしょう?
まず、a,b,c,d,e,fは正の有理数として考えましょう。
どうせ最後に分母をはらえばいいのですから。
もし、上記のような a,b,c,d,e,fがあったとします。
このとき、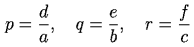 とおくと、
条件から
とおくと、
条件から 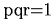 でなければいけません。
でなければいけません。
また、もう一つの条件は 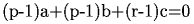 となります。
となります。
つまり、上記のようなa,b,c,d,e,fを求めることは、
「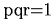 を満たす有理数(p,q,r)」及び、
を満たす有理数(p,q,r)」及び、
「ベクトル(p−1,q−1,r−1)と直交する有理ベクトル(a,b,c)」を求めることに
なります。(完全な1対1ではなく、解全体への全射を作ったことになりますが)
「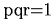 を満たす(p,q,r)」は
を満たす(p,q,r)」は
簡単です。正の有理数p,q,があれば rは自動的に(1/pq)ですから。
また、後半の「ベクトル(p−1,q−1,r−1)と直交する有理ベクトル(a,b,c)」も
かなり簡単です。実際、例外的な事例(p=q=r=1とか)を除けば、
求めるベクトル(a,b,c)全体のなす集合は
(1−q,p−1,0)及び、(0,r−1,1−q)で生成される
有理数上2次元のベクトル空間になります。
あぁ、すっきりした。
私が見つけた中で一番「小さい」のは (2、2、9)と(1、6、6)です。(共に和が13で、積が36)
ということは 3辺の長さが(4、11、11)の三角形と(7、7、12)の三角形は
周の長さと面積が等しいことになります。
もっと「小さい」組はあるでしょうか?
日記トップへ


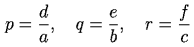 とおくと、
条件から
とおくと、
条件から 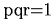 でなければいけません。
でなければいけません。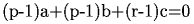 となります。
となります。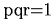 を満たす有理数(p,q,r)」及び、
を満たす有理数(p,q,r)」及び、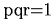 を満たす(p,q,r)」は
を満たす(p,q,r)」は